28. Пространство состояний сети Петри.

Состояние сети Петри определяется маркировкой.

Функция следующего состояния δ : N ⁿ × T → N ⁿ для сети

C = (P, T, I, O) определена, если µ(pi) ≥ #(pi, I(ti))

δ(µ, tj ) = µ’ = µ(pi) − #(pi, I(tj )) + #(pi, O(tj ))

При выполнении сети получаем:

• последовательность маркировок - (µ0, µ1, µ2, . . .)

• последовательность переходов - (t0, t1, t2, . . .)

Инвариант: δ(µ^k , tk ) = µ^k+1

\Состояние сети Петри определяется ее маркировкой. Запуск перехода изменяет состояние сети Петри посредством изменения маркировки сети. Пространство состояний сети Петри, обладаю­щей n позициями, есть множество всех маркировок, т, е. Nⁿ. Из­менение в состоянии, вызванное запуском перехода, определяется функцией изменения б, которую мы назовем функцией следующего состояния. Когда эта функция применяется к маркировке µ (состоя­нию) и переходу tj_t она образует новую маркировку (состояние), которая получается при запуске перехода tj в маркировке µ. Так как tj может быть запущен только в том случае, когда он разрешен, то функция б(µ, tj) не определена, если tj не разрешен в марки ровке µ. Если же tj разрешен, то 6(µ, t_}) = µ', где µ' есть маркиров­ка полученная в результате удаления фишек из входов tj и добав­ления фишек в выходы t_}.

Определение 2.8. Функция следующего состояния б : Nⁿ X Т -> -> Nⁿ для сети Петри С = (Р, Т, I, О) с маркировкой µ и переходом tj € Т определена тогда и только тогда, когда µ(pi) >= #(pi, I(tj)) для всех pi£ Р. Если 6(µ, fj) определена, то б(µ, tj) = µ', где µ'(pi) = µ(pi )- #(pi,I(tj)) + #(рi, 0(tj)) для всех pi£ Р.

Пусть дана сеть Петри С = (Р, Т, I, О) с начальной маркиров­кой µ°. Эта сеть может быть выполнена последовательными запус­ками переходов. Запуск разрешенного перехода tj в начальной маркировке образует новую маркировку р¹ = 6(µ°, tj). В этой новой маркировке можно запустить любой другой разрешенный переход, например t_k, образующий новую маркировку µ² = 6(µ¹, tk). Этот процесс будет продолжаться до тех пор, пока в маркиров­ке будет существовать хотя бы один разрешенный переход. Если же получена маркировка, в которой ни один переход не разрешен, то никакой переход не может быть запущен, функция следующего состояния не определена для всех переходов, и выполнение сети должно быть закончено.

При выполнении сети Петри получаются две последовательности: последовательность маркировок (µ°, µ¹, µ², ...) и последовательность переходов, которые были запущены (tj0, tj1, tj3, ...). Эти две после­довательности связаны следующим соотношением: 6(µ^k, tjk) = p^k+1 для k = 0, 1, 2, ... . Имея последовательность переходов и р°, легко получить последовательность маркировок сети Петри, а имея последовательность маркировок, легко получить последо­вательность переходов, за исключением нескольких вырожденных случаев'). Таким образом, обе эти последовательности представ­ляют описание выполнения сети Петри.

Пусть некоторый переход в маркировке µ разрешен и, следова­тельно, может быть запущен. Результат запуска перехода в марки­ровке р есть новая маркировка µ'. Говорят, что µ' является непо­средственно достижимой из маркировки µ, иными словами, состоя­ние µ' непосредственно получается из состояния µ.

29,30,40 Достижимость сети Петри. + 30.Множество достижимости сети Петри

Достижимость в сети Петри

Для сети C = (P, T, I, O) и µ маркировка µ’ называется непосредственно достижимой из µ, если ∃ tj ∈ T , δ(µ, tj ) = µ’ .

Множество достижимости R(C, µ) - наименьшее множиство маркировок определенных следующим образом:

1. µ Є R(C, µ);

2. если µ' Є R(C, µ) и µ'' = б(µ',t_j) для некоторого t_j Є T, то µ'' Є R(C, µ).

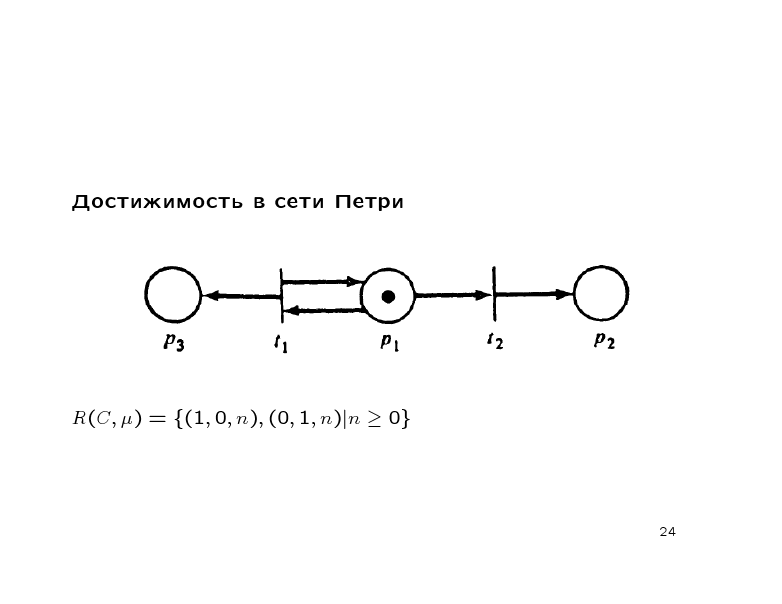
R(C, µ) = {(1, 0, n), (0, 1, n)|n ≥ 0}

ПОДРОБНЫЙ ТЕКСТ:

Определение 1. Для сети Петри С = (Р,Т,I,О, µ) с маркировкой µ маркировка µ' называется непосредственно достижимой из µ, если существует переход t_j Є T, такой, что б(µ,t_j) = µ'. Это понятие легко распространить на определение множества достижимых маркировок данной сети Петри. Если µ' непосредственно достижима из µ', а µ'' из µ', то говорят, что µ'' достижима из µ. Определим множество достижимости R(C, µ) сети Петри С с маркировкой µ как множество всех маркировок, достижимых из µ. Маркировка µ' принадлежит R(C, µ), если существует какая либо последовательность запусков переходов, изменяющих µ на µ'. Отношение "достижимости" является рефлексивным и транзитивным бинарным отношением.

Определение 2. Множество достижимости R(C, µ) для сети Петри С = (P,T,I,O, µ) с маркировкой µ есть наименьшее множество маркировок определенных следующим образом:

1. µ Є R(C, µ);

2. если µ' Є R(C, µ) и µ'' = б(µ',t_j) для некоторого t_j Є T, то µ'' Є R(C, µ).

Пример: рассмотрим сеть Петри. Если маркировка µ = (1,0,0), то непосредственно достижимы две маркировки: (0,1,0) и (1,0,1). Из (0,1,0) нельзя достичь ни одной маркировки, т.к. ни один переход не разрешен. Из (1,0,1) можно получить (0,1,1) и (1,0,2). Вообще говоря, можно показать, что множество достижимости R(C, µ) для этой сети имеет вид: {(1,0,n), (0,1,n)| n>=0}

Для удобства можно распространить функцию следующего состояния на отображение маркировки и последовательности переходов в новую маркировку. Для последовательности переходов (t_j1,t_j2,…,t_jk) и маркировки µ маркировка µ' = б(µ, t_j1,t_j2,…,t_jk) является результатом запусков сначала tl, затем t2 и т.д. до t_jk.

Определение 3. Расширенная функция следующего состояния определяется для маркировки µ и последовательности переходов δ Є Т* следующими соотношениями:

δ(µ,t_j,σ) = δ(δ(µ,t_j),σ), где Т* - множество всех подмножеств множества (булеан множеств) переходов в Т.