14.Способы задания конечных автоматов.

Устройство, оперирующие с логическими сигналами, принимающее только 2 значения – 0 и 1и имеющее некоторое множество внутренних эквивалентных состояний S, множество входных сигналом x и множество выходных сигналов y – называется цифровым автоматом.

Простейшим цифровым автоматом является любое комбинационное устройство, имеющее единственное внутреннее состояние. В этом устройстве каждому набору входных логических переменных соответствует некоторый выходной сигнал. Если автомат может находится в нескольких эквивалентных внутренних состояниях, то его реакция на входные сигналы определяется не только текущим набором входных сигналов, но и внутренним состоянием автомата.

Предполагается, что изменения входных сигналов и внутренних состояний происходит мгновенно, поэтому автомат работает в дискретном времени Ti, где протяженность каждого такта (интервала) может быть сколь угодно большой.

Если в течении времени не произошло изменений входных сигналов x и соответственно внутренних состояний S.

Различают автоматы Мура и автоматы Милли.

Автомат Мура является частным случаем более широкого понятия – автомата Мили.

Автоматы Мура описываются следующими функциями переходов и выходов:

Si+1 = f(Si, xi+1) yi+1 = f(S_i+1)

Каждое новое состояние автомата Мура обусловлено предшествующим состоянием и входным сигналом, а выходная функция – в каждый данный момент времени однозначно определяется состоянием автомата.

Автоматы Мили отличаются от автоматов Мура тем, что выходной сигнал в этом автомате зависит не только от состояния, но и от входного сигнала.

Si+1 = f(Si, xi+1) yi+1 = y(si, xi+1)

Понятие внутреннего состояния автомата предполагает наличие у автомата внутренней памяти. Число различных эквивалентных состояний зависит от глубины памяти.

В качестве элементов памяти могут использоваться стандартные модули ПЗУ или логические схемы с обратными связями в частности – различные типы триггеров.

В принципе любой автомат Мура можно свести к автомату Мили и наоборот.

Автомат Мили – более универсальное устройство

У автомата Мили нет таких ограничений, которые есть у Мура

Задав множество (x s y) достаточно трудно определить как работает конечный автомат. Приведенные выше уравнения, описывающие функционирование автоматов мура и мили устанавливают связь между множествами x s y, но они неудобны для описания функционирования конкретных автоматов, поэтому на практике получили распространение другие способы описания работы конечных автоматов.

Наиболее широко распространены табличное задание, где заданы таблицы переходов и выходов конечного автомата. Здание конечного в виде граф-схемы, а так же задание конечных автоматов в виде ЛГСА (логическая схема алгоритмов).

Рассмотрим задание КА, который для любой пары чисел, записанных в двоичной системе счисления вычисляет и выводит их сумму, при этом данные начинаются с битов, имеющие наименьшие разряды и числа читаются справа-налево.

(в билетах будет пример с триггерами, RS и другие)

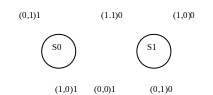
Таблица 2.1

X\S	S0	S1
00 01 10 11	S0	S0
	S0	S1
	S0	S1
	S1	S1

Таблица выходной функции 2.2

X\S	S0	S1
00 01 10 11	0	1
	1	0
	1	0
	0	1

В таблице 2.1 возможные состояния в виде упорядоченной последовательности записаны в 1ой строке.

Входные сигналы в упорядоченном виде записаны в первом столбце.

На пересечении строк и столбцов получаем клетку в которой записано новое состояние.

Таблица переходов (2.1) может быть определена неполностью. В этом случае в таблице имеются прочерки в отдельных клетках.

Некоторые сигналы не вызывают изменения состояния. Так, под действием входных сигналов 0 и 1автомат сохраняет состояние S0, Если он в нем находился и состояние S1, если при подаче такой комбинации входных сигналов он находился в состоянии S1.

Множество выходных сигналов подобным образом задается для каждой пары Si, Lj и на пересечении соответствтвующей строки и столбца получаем выходной сигнал автомата.

Значения выходного сиг нала автомата приведено в таблице 2.2

Иногда, если имеется такая возможность – обе таблицы совмещают.

Для автомата Мура таблица выходов вырождается в одну строку, которую можно записать в первой строке таблицы переходов.

Табличное описание служит удобным формализованным языком, на котором можно задать любой конечный автомат, что дает взаимопонимание между заказчиком и разработчиком.

Распространенное средство описания автомата – логическая граф-схема описания алгоритма.