Тема 2 [3, гл.XI]
Несобственные интегралы
Понятие несобственного интеграла является обобщением понятия определенного интеграла на случай, когда либо подынтегральная функция обращается в бесконечность, либо промежуток интегрирования бесконечен.
Пусть
функция f(x)
задана на [
]
и интегрируема на любом сегменте [
]
при
>
.
Если предел интеграла
при
существует, то его будем называть
несобственным интегралом от функции
f(x)
в пределах от
до
и обозначать символом
Приведем достаточный
признак существования несобственного
интеграла- признак сравнения: если
при
x<
и
существует несобственный интеграл
то существует также несобственный
интеграл
Поэтому существует предел интеграла
при
Пример 6.
Найти несобственный интеграл
.
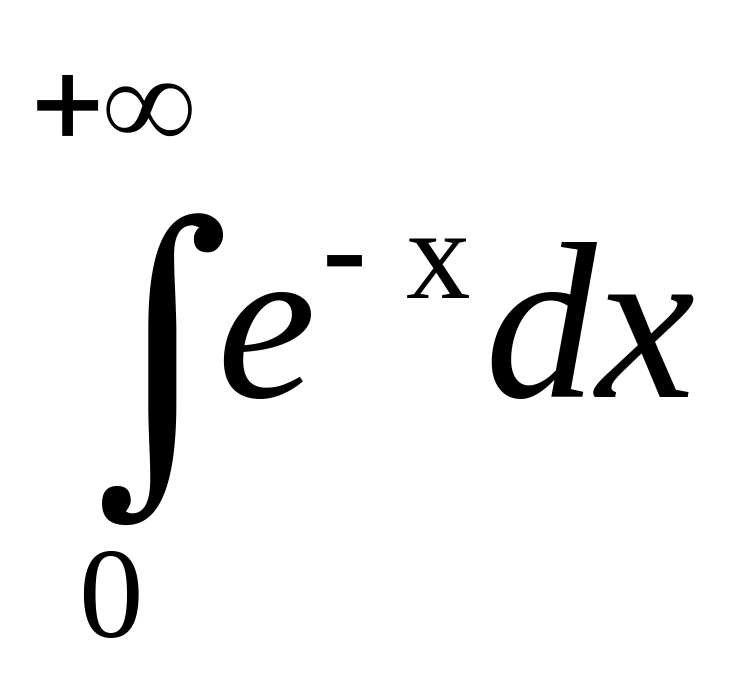Решение. По определению
,
т.е. несобственный интеграл сходится к 1.
Пример
. Покажем, что интеграл
сходится при
>0.
Воспользуемся интегрированием по
частям:
Первое слагаемое
в правой части равенства имеет предел
при x
а
интеграл
сходится на
основании признака сравнения, так как
и интеграл
сходится. Следовательно, существует
предел интеграла
при x
.
Пример 7.
Вычислить несобственный интеграл
.
Решение. По определению ([3], c.382)
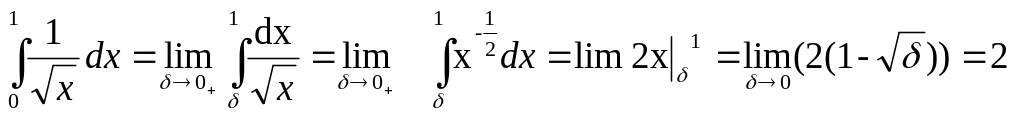,так
как вычисленный
интеграл при
стремится к пределу 2, то несобственный
интеграл
сходится.
Тема 3
Двойной интеграл [1, гл.III]
Рассмотрим на нескольких примерах приемы вычисления двойных интегралов.
Пример 8.
Вычислить повторный интеграл
,
затем изменить порядок интегрирования,
вычислить полученный интеграл и сравнить
ответы.
Решение.
а)
б) Строим
область интегрирования (заштрихованная
рис.1) согласно заданным пределам по x
и по y
и меняем порядок интегрирования .Эту
область разобъем отрезком прямой y=1
(x
на две замкнутые области D
.
В D
y
изменяется от 0 до 1, а x
изменяется от 0 до y.
В D
имеем 1
.
Окончательно поучим:
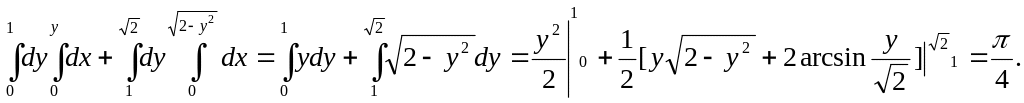
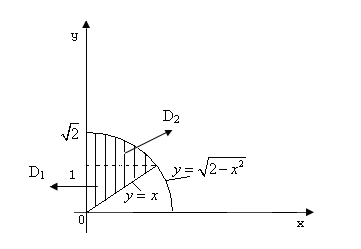
Рис.1
Пример 9.
Вычислить двойной интеграл
по области
.
Решение. Представим двойной интеграл в виде повторного: сначала по х, затем по у (рис.2)
Рис. 2
Интеграл
найдём по частям.
Интеграл
.
Поэтому
.
Тема 4 [4,гл.XIII]
Дифференциальные уравнения
Простейший пример дифференциального уравнения первого порядка первой степени, разрешенное относительно производной, имеет вид
.
Функция f(x) предполагается непрерывной на некотором интервале (a,b) оси x. Пользуясь другим обозначением производной, можно записать это уравнение в виде
Множество решений этого уравнения даётся формулой
(1)
где с- произвольная постоянная.
Пример 10. Найти общее решение уравнения
.
Решение.
Согласно (1) имеем
Уравнения вида
(2)
называются
уравнениями с разделенными переменными.
Функции
будем считать непрерывными.
Пример 11. Найти общее решение дифференциального уравнения
y′=0.
Решение. Перепишем его в виде
2x(1+y
)+
=0.
Домножим обе части на dx≠0 и получим
2x(1+y )dx+ dy=0.
Это уравнение с разделяющимися переменными.
Левую и правую
части полученного уравнения разделим
на (1+y
и проинтегрируем:
,
arctgy-2
=C.
Пример 12. Найти общий интеграл уравнения
y′=
.
Решение.
Это уравнение является однородным, так
как сводится к виду y′=f(
Разделим числитель
и знаменатель исходной дроби на
≠0.
Получим:
y′=
Замена
Тогда y=x·t(x) и y′=1+x·t′.
Следовательно
t+xt′=
x·
.
Разделяем переменные x,t и интегрируем:
2arctgt-3ln(t
=ln
+c.
Возвращаясь к старым переменным y и x, получим
2 arctg
c.
Дифференциальные уравнения n-ого порядка
Пусть дано линейное дифференциальное уравнение n-го порядка с постоянными коэффициентами и произвольной правой частью f(x):
y
′+a
y=f(x).
(1)
Зная фундаментальную систему решений соответствующего однородного уравнения
y ′+a y=0, (2)
можно найти и
решение неоднородного уравнения (1). Мы
применим при этом метод вариации
произвольных постоянных. Суть метода
состоит в следующем. Вначале решаем
однородное уравнение (2). Пусть y
-
линейно независимые решения уравнения
(2). Тогда y
-
общее решение однородного уравнения
(2). На следующем шаге константы
варьируем, то есть, считаем
-
неизвестные функции аргумента x
и ищем общее решение неоднородного
уравнения (1) в виде
y=
Функции
определяются из системы уравнений
(3)
Затем, интегрируя,
находим сами функции
с точностью до произвольных постоянных
соответственно.
Пример 11. Решить
уравнение y"-
2y′
-3y
=
.
Решение.
Составим характеристическое уравнение
,решив
которое будем иметь
.
Общее решение находим в виде
Система уравнений (3) будет иметь вид
и решая эту систему, получаем
или после интегрирования
общее решение данного уравнения
или
Контрольная работа №3
Задание 3.1. Найти неопределенные интегралы, пользуясь свойствами линейности, методами подстановки и интегрированием по частям .
Задание 3.2. Вычислить несобственные интегралы.
Задание 3.3. Вычислить указанные двойные интегралы, затем переменить порядок интегрирования и сравнить ответы.
3.3.1.
,
3.3.2.
,
3.3.3.
,
3.3.4.
,
3.3.5.
,
3.3.6.
,
3.3.7.
,
3.3.8.
,
3.3.9.
,
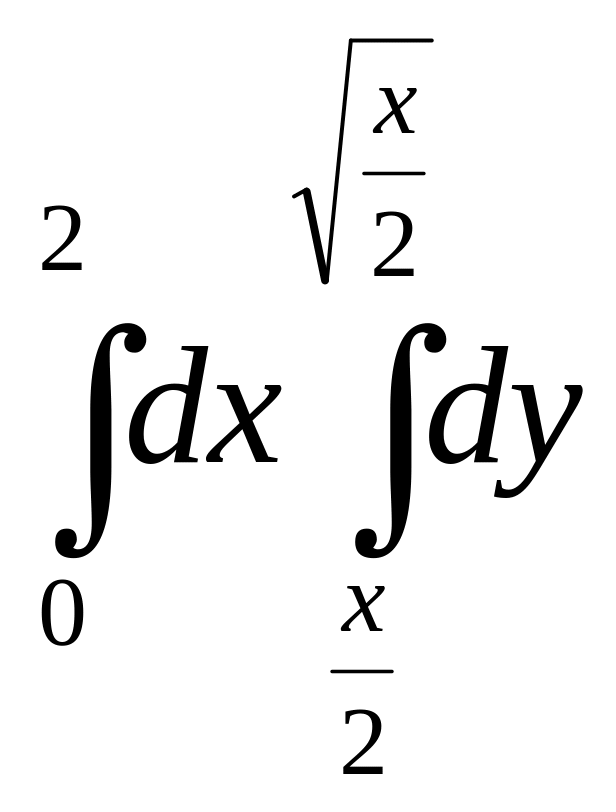3.3.10.
,
3.3.11.
,
3.3.12.
,
3.3.13.
,
3.3.14.
,
3.3.15.
,
.3.16.
,
3.3.17.
,
3.3.18.
,
3.3.19.
,
3.3.20.
,
3.3.21.
,
3.3.22.
,
3.3.23.
,
3.3.24.
,
3.3.25.
,
3.3.26.
,
Задание 3.4. Найти общее решение дифференциального уравнения
первого порядка.
Задание 3.5.Определить решение неоднородного дифференциального уравнения методом вариации произвольных постоянных
3.5.1. y"+y=xlnx+
,
3.5.2.
,
3.5.3.
,
3.5.4.
,
3.5.5.
,
3.5.6.
3.5.7.
,
3.5.8.
,
3.5.9.
3.5.10.
3.5.11.
,
3.5.12.
,
3.5.13.
,
3.5.14.
,
3.5.15
,
3.5.16.
,
3.5.17.
,
3.5.18.
,
3.5.19.
,
3.5.20.
,
3.5.21.
,
3.5.22.
,
3.5.23.
,
3.5.24.
,
3.5.25.
.
3.5.26.
