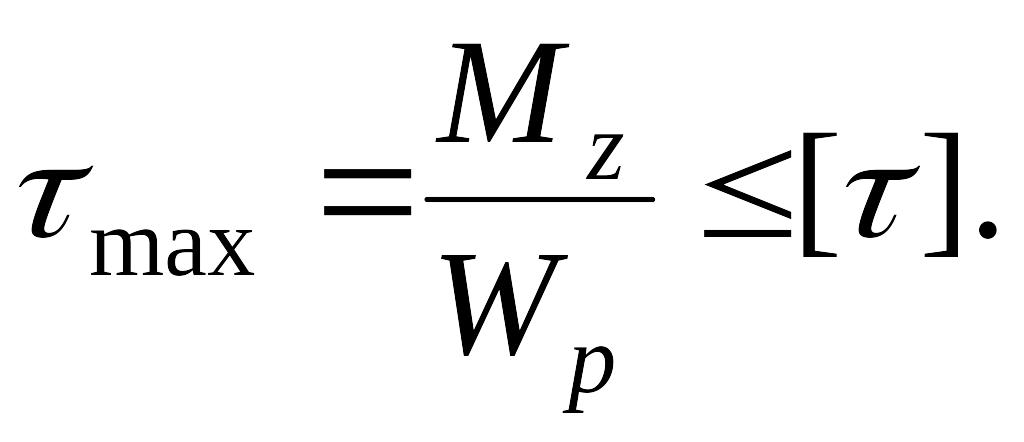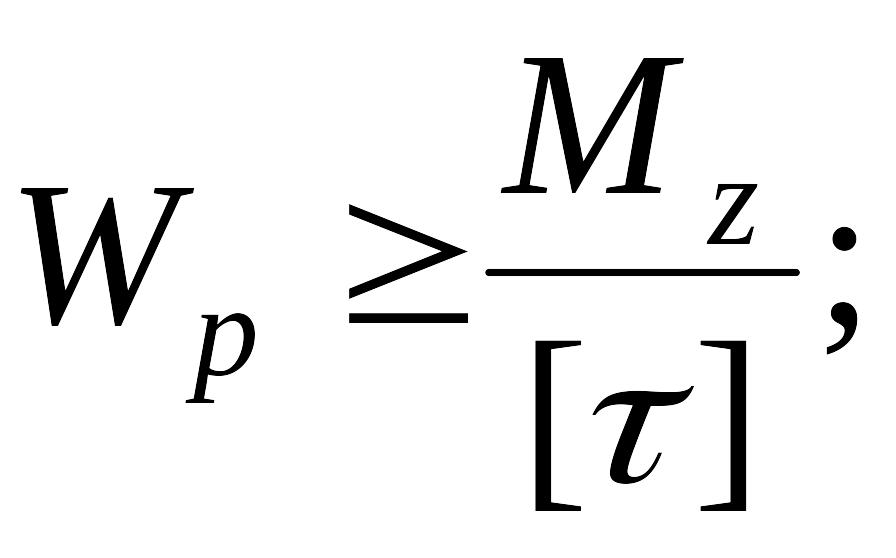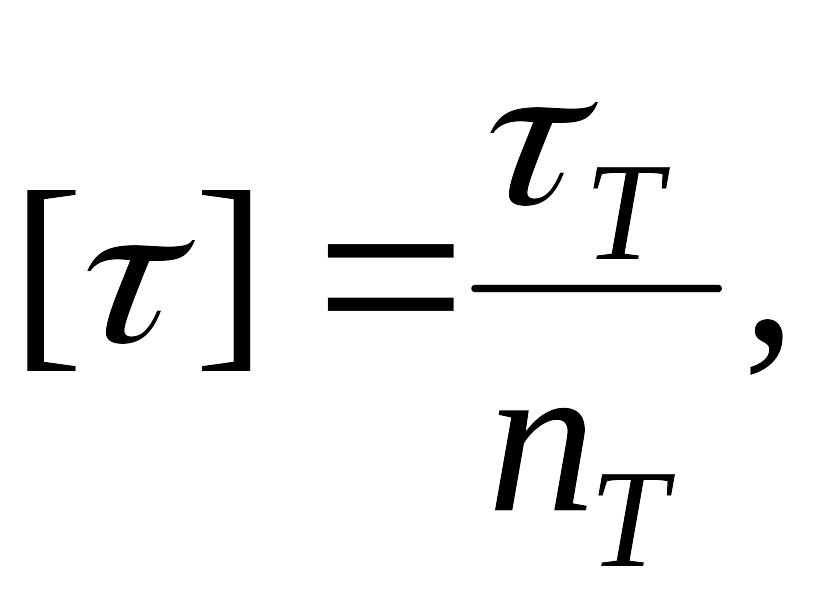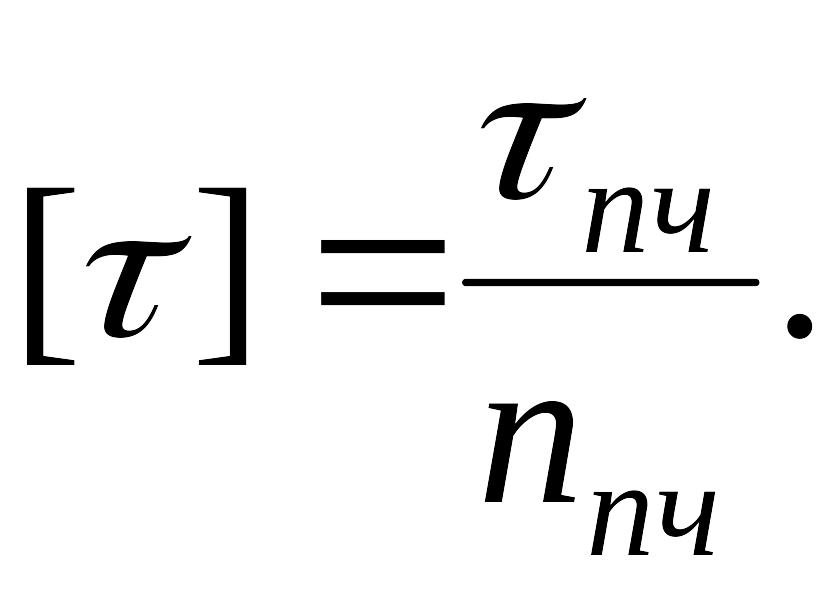23. Полярный момент инерции.

Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется физическая величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где:

• m_i — масса i-й точки,

• r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

,

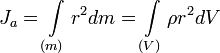где:

• dm = ρdV — масса малого элемента объёма тела dV,

• ρ — плотность,

• r — расстояние от элемента dV до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

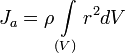
24. Расчетные формулы на прочность и жесткость при кручении.

Прочность бруса, работающего на кручение, считают обеспеченной, если наибольшие касательные напряжения, возникающие в его опасном поперечном сечении, не превышают допускаемых:

Эта формула выражает условие прочности при кручении бруса круглого (кольцевого) сечения и служит для выполнения проверочного расчета.

Для проектировочного расчета и для определения допускаемой нагрузки (момента) из формулы (7.14) соответственно получаем

	(7.15)
	(7.16)

Крутящий момент , который входит в приведенные расчетные формулы, с помощью метода сечений должен быть выражен через внешние (скручивающие) моменты.

Расчет ведется для опасного поперечного сечения. Для бруса постоянного диаметра опасным является сечение, в котором возникает наибольший крутящий момент. Если диаметр бруса не постоянен, может оказаться, что наибольшие напряжения возникают не там, где крутящий момент максимален, следовательно, в этом случае вопрос об опасном сечении дол­жен быть исследован дополнительно (пример 7.1).

Допускаемое напряжение для пластичных материалов назначают в зависимости от их предела текучести на кручение (на сдвиг) , т. е.

(7.17)

а для хрупких материалов — в зависимости от предела прочности:

(7.18)

Для пластичного материала диаграмма зависимости между касательным напряжением и углом сдвига (характеристика материала при сдвиге), полученная путем соответствующей обработки результатов испытаний на кручение, показана на рис.7.11. Площадка текучести на этой диаграмме отсутствует. В качестве предела текучести условно принимают напряжение, при котором остаточный угол сдвига равен 0,003 радиана.

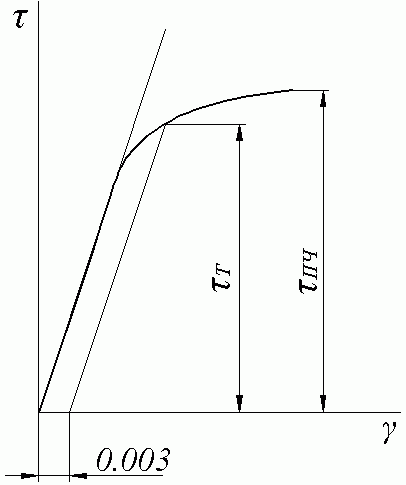
Рис.7.11. Диаграмма испытаний на кручение

25. Виды соединений деталей машин

Соединения деталей, применяемые в машино- и приборостроении, при­нято делить на подвижные, обеспечивающие перемещение одной дета­ли относительно другой, и неподвижные,в которых две или несколь­ко деталей жестко скреплены друг с другом (рис. 88).