Определение устойчивости по логарифмическим характеристикам

Для устойчивости замкнутой системы необходимо и достаточно, чтобы ЛАЧХ разомкнутой системы пересекала ось частот раньше чем ЛФЧХ линию фазового сдвига –π.

Для устойчивости необходимо и достаточно, чтобы частота среза располагалась левее точки пересечения ЛФЧХ с линией фазового сдвига –π.

Для устойчивости замкнутой системы необходимо и достаточно, чтобы при положительных значениях ЛАЧХ разность между числом положительных(снизу вверх) и отрицательных(с верху вниз) переходов фазочастотной характеристики линии фазового сдвига –π равнялась l/2, где l – число правых корней характеристического уравнения разомкнутой системы. Начало характеристики на линии фазового сдвига принимается за 0,5 перехода.

Логарифмический критерий устойчивости позволяет просто определить запасы устойчивости системы по амплитуде.

h1, h2– запас устойчивости системы по амплитуде.

Φ – запас устойчивости системы по фазе.

Точность сау

Различают точность, рассматриваемую в переходном процессе - динамическая точность, и точность в установившемся режиме - статическая точность.

Проще всего рассмотреть понятие точности на примере следящей системы. Для этого наилучшим образом применима передаточная функция по ошибке, позволяющая записать сигнал ошибки при любом виде задающего воздействия: (p) = W_(p) U^зад(p) + W_f(p) f(p).

Общий способ повышения точности (в статическом и динамическом режимах) – обеспечение следующих оценок:

W_зс(p) = W(p)/(1+W(p)  1 - Мера точности воспроизведения задающего воздействия в замкнутой системе.

W_с(p) = 1/(1+W(p)  0 - Мера малости ошибки слежения

Статическая точность в следящей системе определяется при гармоническом входном воздействии с использованием передаточной функции по ошибке. p W_c(p) U^зад(p), W_c(p) = 1/(1+W(p)).

Один из основных способов повышения точности - увеличение коэффициента k разомкнутой системы. Однако это не значит, что можно таким образом достичь любой желаемой точности. При чрезмерном увеличении k возможна потеря устойчивости замкнутой системы. Повышение точности всегда приводит к уменьшению запаса устойчивости по амплитуде.

Динамическая точность относится к более сложным задачам анализа систем, т.к. требует изучения всего переходного процесса. Для повышения динамической точности системы обычно используется принцип комбинированного управления по задающему воздействию (принцип инвариантности).

Добавим в стандартную структуру системы дополнительную передаточную функцию (p)  1/(W(p)W_oc(p)) так, чтобы сигнал ошибки вообще не зависел от задающего воздействия. Это можно выполнить введением в систему дополнительной ветви прохождения сигнала, и подобрать коэффициент передачи в этой ветви так, чтобы компенсировать нежелательный сигнал.

Построение желаемой характеристики системы

Под желаемой понимается такая логарифмическая амплитудно-частотная характеристика ЛАЧХ разомкнутой системы, которая обеспечивает заданные показатели качества системы в замкнутом состоянии. Строится на основе заданных показателей качества проектируемой системы:

1. Величина перерегулирования – σ . %

2. Время регулирования – tР с.

3. Коэффициент передачи разомкнутой системы K

Желаемая логарифмическая амплитудно-частотная характеристика

L_C(ω) может быть разбита на три характерных участка: низкочастотный, среднечастотный и высокочастотный, причем вид характеристики зависит от типа системы.

НЧ–асимптота определяет точность системы в установившемся режиме

и поэтому НЧ–асимптота желаемой ЛАЧХ должна совпадать с низкочастотной асимптотой ЛАЧХ нескорректированной системы, считая, что коэффициент усиления нескорректированной системы соответствует требуемой точности. Низкочастотный участок определяет точность воспроизведения

системой медленно меняющихся воздействий.

СЧ–асимптота желаемой ЛАЧХ определяет качество переходного процесса и запасы устойчивости системы и строится на основе заданных показателей качества переходного процесса: времени регулирования tР и величины максимального перерегулирования σ. При этом определяются частота среза ωС , сопрягающие частоты ω2 и ω3 СЧ–асимптоты из условия

-L₁ ≤L_С(ω) ≤+ L₁, а также находится значение необходимого запаса по фазе γ.

Высокочастотный участок очень мало влияет на переходный процесс и строится прямыми с наклоном –40 или –60 дБ/дек или с наклоном

меньшим на 20 дБ/дек, чем ЛАЧХ нескорректированной системы на этом

участке.

Среднечастотный участок сопрягается с соседними либо непосредственно путем продолжения СЧ участка, либо с помощью сопрягающих прямых, имеющих наклон –40 или –60 дБ/дек.

Желаемая характеристика L_C(ω) строится так, чтобы она по возможности меньше отличалась от ЛАЧХ нескорректированной системы L_Н(ω). При этом получается корректирующее устройство наиболее простого типа. Для этого допустимо увеличить запасы устойчивости, изменить наклон сопрягающих прямых и наклон ВЧ–части.

После построения желаемой характеристики LС(ω) необходимо построить фазовую характеристику ϕС(ω) и определить запас по фазе Δϕ, кото-рый должен удовлетворять условию Δϕ≥ γ.

Правила преобразования схем нелинейных САУ

Принцип суперпозиции не выполняется

 

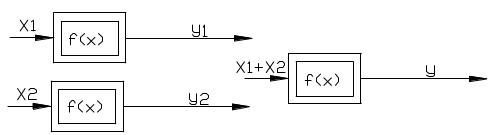
y=y1+y2 , для линейных систем (принцип выполняется );

y<>y1+y2 для нелинейных САУ.

1)    в линейной части системы можно производить любые структурные преобразования.

2)    нельзя переставлять Н.Э. между собой

3)    нельзя переставлять линейные и Н.Э.

4)    нелинейные статические элементы можно переносить через узел ветвления.

 При переносе статического нелинейного элемента через узел по (против) направления передачи сигнала в отходящую от узла ветвь следует добавить нелинейный элемент с прямой (обратной) характеристикой.

 

Классификация дискретных систем

Рассмотрим системы автоматического управления, в которых передача, обработка и преобразование информации осуществляются только в определенные моменты времени, то есть дискретно. В этом случае в системах действуют сигналы, являющиеся некоторой последовательностью импульсов, и такие системы называются дискретными. Создание дискретных систем может быть вызвано многими причинами:

1) принцип действия некоторых элементов, входящих в систему, может быть дискретным, поэтому и вся система управления будет дискретной.

2) в дискретных системах проще реализовать сложные алгоритмы управления.

3) точность решения алгоритмов управления с помощью дискретных устройств обычно выше, чем с помощью непрерывных

дискретные системы можно разделить на линейные и нелинейные (в зависимости от применимости к ним принципа суперпозиции) и на стационарные и нестационарные (по степени изменения параметров во времени). Следует четко различать такие понятия, как процесс и сигнал. Процесс отображает ту информацию, которая преобразуется системой, а сигнал является физическим носителем этой информации.

Преобразование непрерывных процессов в дискретные называется квантованием. Существует три вида квантования: по времени, по уровню и по времени и уровню одновременно. При квантовании по времени исходная непрерывная функция x(t) преобразуется в последовательность дискретных значений x(ti), где ti-это дискретные моменты времени на временной оси. При квантовании по уровню вся область возможных х разбивается на отдельные дискретные уровни и дискретный процесс может принимать только те значения, которые совпадают с выбранными уровнями. Информация о значениях дискретного процесса передается с помощью импульсных сигналов путем модуляции (процесс преобразования первичного сигнала) их параметров: амплитуды, длительности, фазы, частоты. Отсюда различают системы с амплитудной, широтной, фазовой и частотной модуляциями.

Z – преобразование

дискретное преобразование Лапласа произвольной решетчатой функции f[k] определяется соотношением

Оператор e^–sT в этой формуле имеет смысл оператора запаздывания на время одного шага Т. обозначая e^sT сокращенно символом z, мы приходим к z-преобразованию, для которого формула прямого преобразования имеет вид

Z-пребразование дает возможность получить из X(z) значение ординат решетчатой функции x[nT] в моменты квантования. Основные теоремы z-преобразования:

1. Свойство линейности

Если F1(z,σ)=Zσ {f1(t)} и F2(z,σ)=Zσ {f2(t)}, то Zσ {a1f1(t) + a2f2(t)}= a1 F1(z,σ) + a2 F2(z,σ).

2. Теорема сдвига (смещения)

Если Zσ {f(t)} = F(z,σ) и τ - произвольное положительное число, тогда

3. Изображение обратных разностей

4. Изображение конечных сумм

5. Предельные значения.