Временные характеристики сау

Временной характеристикой системы называется закон изменения выходной величины в функции времени при изменении входного воздействия по определенному закону и при условии, что до приложения воздействия система находилась в покое. Временные характеристики определяются как реакция системы на типовые воздействия при нулевых начальных условиях.

К основным временным характеристикам относятся переходная функция и функция веса.

Типовые воздействия. В качестве типовых воздействий при исследовании систем используются:

– единичная функция;

– единичный импульс;

– линейно – растущее воздействие;

– квадратичное воздействие;

– гармоническое воздействие.

Переходная функция. Переходная функция h(t) – реакция системы на единичное воздействие при нулевых начальных условиях.

Весовая функция. Весовая функция k(t) – реакция системы на единичный импульс при нулевых начальных условиях.

Методы определения временных характеристик

1. Классический метод (основан на решении дифференциальных уравнений).

2. Операторный метод, использующий разложение на простые дроби.

3. Операторный метод, использующий вычеты.

4. Метод аналогового и цифрового моделирования.

5. Метод трапеций.

Интегрирующее звено

Звено описывается уравнением .

Или в другой форме записи , откуда и получилось название звена. В идеальном интегрирующем звене выходная величина пропорциональна интегралу по времени от входной или скорость изменения выходной величины пропорциональна входной величине звена.

Передаточная функция звена . Его частотные и временные функции имеют следующий вид:

Примерами интегрирующего звена являются: резервуар, наполняемый жидкостью; электродвигатель постоянного тока; гидроцилиндр с распределительным золотником, операционный усилитель в режиме интегрирования.

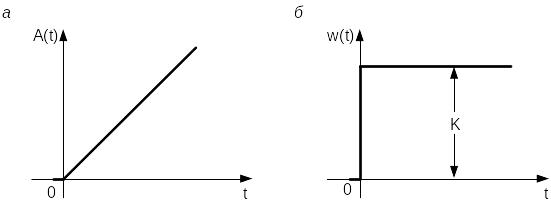
Переходная функция (а) и дельта-функция (б) интегрирующего звена

Амплитудно-фазовая характеристика для положительных частот сливается с отрицательной частью оси мнимых.

Построение ЛАХ выполняется по выражению . Нетрудно видеть, что ЛАХ представляет собой прямую с отрицательным наклоном 20 дБ/дек, пересекающую ось нуля децибел при частоте среза _ср = k. ЛФХ представляет собой прямую  = – 90, параллельную оси частот.

Апериодическое звено

Звено относится к группе позиционных звеньев и описывается уравнением (4.3).Передаточная функция этого звена .

Одним из примеров апериодического звена является RL–цепь, где входной величиной является напряжение U₁, поступающее на цепь, а в качестве выходной величины может рассматриваться ток или напряжение U₂ на сопротивлении R.

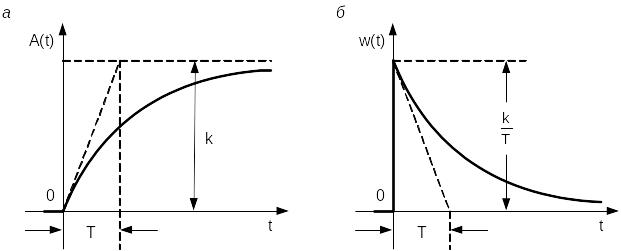
Переходная функция звена найдется как решение уравнения (4.3) при x₁ = 1 и начальном условии x₂ = 0 при t = 0.

Отрезок, отсекаемый касательной к кривой, в любой точке кривой на асимптоте равен постоянной времени T. Видно, что чем больше постоянная времени звена, тем больше длится переходный процесс, то есть медленнее устанавливается статическое значение x₂ = k на выходе звена.

Его частотные функции имеют следующий вид:

АФЧХ для положительных частот имеет вид полуокружности с диаметром, равным коэффициенту передачи звена k .Величина постоянной времени звена Т определяет распределение отметок  вдоль кривой.

ЛАХ, ЛФХ: