20 Критерии устойчивости. Определение устойчивости по логарифмическим характеристикам.

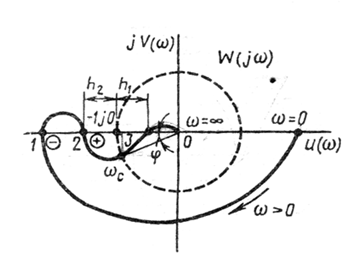
Для устойчивости замкнутой системы необходимо и достаточно, чтобы ЛАЧХ разомкнутой системы пересекала ось частот раньше чем ЛФЧХ линию фазового сдвига –π.

Для устойчивости необходимо и достаточно, чтобы частота среза располагалась левее точки пересечения ЛФЧХ с линией фазового сдвига –π.

Для устойчивости замкнутой системы необходимо и достаточно, чтобы при положительных значениях ЛАЧХ разность между числом положительных(снизу вверх) и отрицательных(с верху вниз) переходов фазочастотной характеристики линии фазового сдвига –π=l/2, где l – число правых корней характеристического уравнения разомкнутой системы. Начало характеристики на линии фазового сдвига принимается за 0,5 перехода.

Логарифмический критерий устойчивости позволяет просто определить запасы устойчивости системы по амплитуде.

h1, h2– запас устойчивости системы по амплитуде.

Φ – запас устойчивости системы по фазе.

Необходимые значения запаса устойчивости зависят от классов систем и требований к качеству регулирования.

Ориентировочно: Δφ(w)=30..60⁰; Δl(w)=6..20 дб.

21 Точность сау. Статические и астатические системы.

Точность линейной системы управления:

;

Ошибка регулирования может быть определена в системе с использованием теоремы оконечных значениях преобразования Лапласа.

– теорема

Из теоремы

Ошибка регулирования зависит от динамических свойств и от выходной характеристики.

1) Ступенчатое воздействие.

1.1) Статическая: W(p)=B(p)/A(p);

– статическая ошибка.

1.2) Астатизм 1-го порядка ;

– статическая ошибка по возмущающему воздействию

2) Инерционное воздействие.

2.1 статическая W(p)=B(p)/A(p)

В статической системе при линейном воздействии внешнего регулирования будет достигнуто нелинейное значение

2.2 Астатическая система. ν=1: W(p)=B(p)/pA(p);

– скоростная ошибка

2.3 Астатическая система. ν=2: W(p)=B(p)/pA(p);

22 Методы повышения точности сау.

1)Увеличение общего коэффициента системы.

Чрезмерное увеличение коэффициента усиления может привести к потере устойчивости системы.

2) Увеличение порядка астатизма системы.

Ввели звено W₃

W(p)=kk₁/p2(Tp+1); C(p)=p2(Tp+1)+kk₁

Tp3+p2+kk₁=0 – система не устойчива.

Однако увеличение порядка астатизма системы может привести к потере устойчивости.

В строго неустойчивых система устойчивость не может быть достигнута лишь изменением параметров элементов системы, а требует введения дополнительных звеньев

3) Введение изодромных звеньев.

W(p)=kk₁k₂(τp+1)/[p²(Tp+1)]

C(p)=Tp³+p²+kk₁k₂τp+ kk₁k₂

Введение изодромного звена позволяет уменьшить ошибку регулирования за счет увеличения порядка астатизма и одновременно обеспечить устойчивость системы.

4) Коррекция задающего воздействия(введение масштабируемых звеньев) позволяет придать системе астатические свойства или повысить порядок астатизма относительно задающего воздействия.

в этом случае ошибка равна нулю

–корректирующее устройство

Астатизм системы обеспечивается только при точном значении коэффициента передачи корректирующего звена расчетным.

5) Неединичная обратная связь так же позволяет обеспечить астатизм системы относительно задающего воздействия.

В системе без интегрирующих звеньев соответствующим выбором коэффициента основной и обратной связи может быть обеспечен астатизм относительно задающего воздействия.

Как и в предыдущем случае нестабильность коэффициентов К может служить причиной появления статической ошибки слежения