Лабораторная работа №1 измерение давления и расхода, определение режима течения жидкости

Цели работы:

• Изучение основных величин гидравлики и аналогий между системами различной физической природы;

• Изучение приборов и единиц измерения давления и расхода;

• Экспериментальное определение режима течения жидкости.

Теоретические основы:

При движении вязкой жидкости различаются два режима - ламинарный и турбулентный.

Ламинарный поток имеет слоистую структуру - частицы жидкости дви­жутся с различными скоростями параллельно оси трубы без перемешива­ния и без пульсаций скорости и давления.

Турбулентный поток характеризуется неупорядоченным движением частиц жидкости. Наряду с основным поступательным перемещением частиц жидкости вдоль трубы наблюдаются хаотичные поперечные перемеще­ния и вращательные движения частиц, которые приводят к интенсивному перемешиванию жидкости. Кроме того, в каждой точке турбулентного потока наблюдаются пульсации скорости и давления.

Опытами установлено, что переход от ламинарного движения к тур­булентному происходит внезапно, скачкообразно, при определенном зна­чении безразмерного параметра. Данный безразмерный параметр получил название числа Рейнольдса:

(1)

Здесь  - средняя скорость потока, м/с;

d - диаметр трубы, м;

 - кинематическая вяз­кость жидкости, м²/с.

Для каждой конкретной установки существует некоторый диапазон значений числа Re, которые можно рассматривать как критические значения Re_кр, при которых и происходит смена режимов движения. На значение критического числа Рейнольдса существенное влияние оказывают различные возмущения, возникающие в потоке вследствие особенностей структуры течения до входа в трубу и при входе (сужение потока и т.п.).

Необходимо иметь в вицу, что переход ламинарного движения к турбу­лентному удается задержать до достижения весьма больших значений Re, в то время как восстановление ламинарного движения при переходе к нему от турбулентного осуществляется при относительно малых значе­ниях Re. В практике гидравлических расчетов именно это малое зна­чение Re и принимают за Re_кр.

При движении жидкости в круглых трубах принимают Re_кр = 2320. Таким образом, при Re < Re_кр в потоке сохраняется ламинарный ре­жим, а при Re > Re_кр - турбулентный. Переход ламинарного режима в турбулентный происходит при увеличении скорости потока (расхода), а также при уменьшении вязкости жидкости и поперечных размеров потока (при постоянном расходе).

Если в начале и конце трубы установить пьезометры, то разность пьезометрических напоров h₁ в начале и h₂ в конце трубы покажет величину потери напора на трение h_l при движении на расстояние l между сечениями 1-1 и 2-2 (рис. 4).

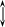
1

2

l

1

2

Рис. 2. Схема измерения потери напора на трение по длине трубы.

Зависимость гидравлических потерь на трение от скорости потока имеет вид:

(2)

где a - коэффициент пропорциональности;

n - показатель степени.

При ламинарном режиме потери на трение пропорциональны средней скорости потока (n=1). При турбулентном режиме с увеличением числа Рейнольдса показатель степени в формуле (2) возрастает от n=1,75 до n=2. Нижний предел этого интервала соответствует области сопротивления гидравлически гладких труб, верхний предел - квадратичному закону сопротивления (гидравлически шероховатым трубам). Промежуточные значения характеризуют переходную область сопротивления.

Экспериментальная часть:

Для проведения эксперимента необходимо:

1. Включить питание стенда;

2. Включить электродвигатель (кнопка “Пуск”);

3. Включить распределитель (тумблер Р1 в верхнее положение);

4. Дать возможность поработать стенду в течение 5 – 6 минут;

5. Произвести замеры времени прохождения заданного объема рабочей жидкости через трубопровод аб (внутренний диаметр трубопровода – 6 мм). Время измерять с помощью электронного секундомера, а объем проходимой жидкости измерять с помощью расходомера (один поворот красной стрелки на расходомере соответствует прохождению через устройство одного литра жидкости). Опыты провести при различных расходах (расход изменяется с помощью регулятора расхода РР). В каждом опыте необходимо также фиксировать температуру рабочей жидкости.

После проведения всех опытов необходимо отключить питание секундомера, выключить электродвигатель и отключить питание стенда.

Обработка результатов опыта:

1. Вычислить кинематическую вязкость масла М-8В (залитого в системе стенда) по эмпирической формуле:

ν = 11,8·10-6 (50/ Т)1,79

(3)

где ν - кинематический коэффициент вязкости, м²/с;

Т - температура, °С.

2. Определить расход масла:

(4)

и записать данные в таблицу 1

3. Рассчитать среднюю скорость жидкости

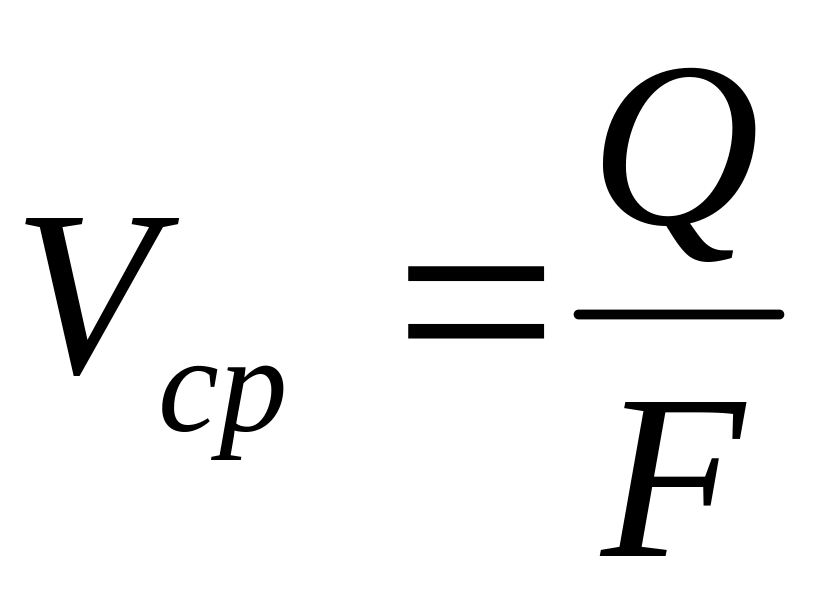
где площадь проходного сечения трубопровода, м².

4. Рассчитать число Рейнольдса по формуле (1)

5. Определить режимы течения жидкости в трубопроводе для всех случаев.

6. Сделать выводы.

Таблица 1

№ опыта	tж, ºC	t, с	W, м3	Q, м3/с	Vср, м/с	ν, м2/с	Re	Режим течения
1.
2.
3.
4.