Экзаменационные задачи

по курсу «Математический анализ». (второй семестр)

Э1.

1. Найти: .

2. Доказать равенство: .

Вычислить:

3. . 4 .

5 Найти: .

Пользуясь первой теоремой о среднем, оценить интегралы:

6. . 7. .

Доказать: 8. . 9. .

Найти площади фигур, ограниченные кривыми:

10. xy = a², xy = 2a ², y = x, y = 2x, (x > 0, y > 0).

11.  = acos4. 12. x⁴ + y⁴ = 2a²xy.

Найти центр тяжести однородной пластины:

13. x = a(t – sint), y = (1 – cost), t[0, 2], y = 0.

14.  = a(1+cos),  = 0.

15. Найти центр тяжести контура сферического треугольника:

x² + y² + z² = a², x  0, y  0, z  0.

Э2.

1.Вычислить моменты инерции относительно координатных осей одного витка винтовой линии: x = acost, y = asint, z = ,

0  t  2.

2. Найти длину дуги кривой:

x = e ^tcost, y = e ^tsint, z = e ^t, -  t  0.

Доказать равенства:

3. = . 4. .

Вычислить:

5. . 6. .

7. ; .

Исследовать интегралы на сходимость:

8. . 9. . 10. .

Исследовать интегралы на абсолютную и условную сходимость:

11. . 12. . 13. , q  0.

14. Исследовать ряд на сходимость.

15. Исследовать ряд на сходимость: .

Э3.

Исследовать ряды на абсолютную и условную сходимость:

1. . 2. .

Найти du и d²u, если:

3. u = (, );  = ax + by + cz,  = x + y + z.

4. u = (, , );  = ax,  = by,  = cz.

5. u = (t); t = x² + y² + z².

6. u = f(x + y + z, x² + y² + z²).

7. u = f(, );  = x + y,  = x – y.

8. u = f(, , );  = x² + y²,  = x² – y²,  = 2xy.

9. u = f(x + y, z).

10. Найти , если x² + y² + z² = 2z.

11. Найти , если u = (х + у).

12. Найти , если x³ + y³ + z³ – 3z = 0.

13. Найти , если xu + yv = 0; uv – xy = 5.

14. Вычислить , если u = (х у).

15. Найти z_x и z_y в точке u = 1, v = 1, если x = u + lnv, y = v – lnu, z = 2u + v.

Э4.

1. Найти z_xу в точке u = 2, v = 1, если x = u + v², y = u² – v², z = 2uv.

Написать разложение в ряд Тейлора следующих функций в окрестностях указанных точек:

2. , .

3. , .

4. , .

5. , .

6. Перейти к полярным координатам в выражении:

.

7. В уравнении х ²у + 3ху + у = 0 сделать замену независимой переменной х = е^t.

8. Заменив переменные  = x,  = y – bz, решить уравнение:

, а 0.

9. После замены переменных  = x,  = решить уравнение:

.

10. Приняв у за новую независимую переменную, преобразовать уравнение

у – ху ³ + е^уу ³ = 0.

11. В уравнении: , сделать замену переменных, полагая:

, , .

12. В уравнении сделать замену переменных .

13. Перейти к полярным координатам в выражении: .

14. Перейти к полярным координатам в уравнении: (ху – у )² = 2ху(1 + у²).

15. Решить уравнение , полагая  = х,  = у/х.

Э5.

Исследовать на экстремум функции:

1. z = x⁴ + y⁴ – 2x² – 4xy – 2y². 2 . u = xy²z³(5 – x – 2y – 3z), a > 0.

3. Исследовать на экстремум функцию z = z(x, y), определяемую неявно уравнением

(x² + y² + z²)² = a²(x² + y² – z²).

Найти условный экстремум функции:

4. z = x² + 12xy + 2y², если x² + y² = 2, y + z = 2, x, y, z > 0.

5. u = xyz, если x² + y² + z² = 1, x + y + z = 0.

Найти sup и inf функции:

6. u = x² – xy + y², если | x | + | y |  1.

7. u = (x + y + z)e^{–(x + 2y + 3z)} , если x > 0, y > 0, z > 0.

8. u = x² + 2y² + 3z², если x² + y² + z²  100.

9. Вписать в круг треугольник, с наибольшей суммой квадратов сторон.

В следующих интегралах изменить порядок интегрирования:

10. . 11. .

12. . 13. . 14. .

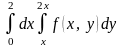Расставить пределы интегрирования в полярной системе координат:

15. .

Э6.

1. Расставить пределы интегрирования в полярной системе координат: .

Вычислить интегралы:

2. . 3. .

4. .

5. , {y² = 2x, x + y = 4, x + y = 12}.

6. .

7. .

8. .

Вычислить объемы тел, ограниченных поверхностями:

9. z = x² + y², x² + y² = x, x² + y² = 2x, z = 0.

10. x² + z² = a², x + y =  a, x + y =  a.

11. z = 1 + x + y, z = 0, x + y = 1, x = 0, y = 0.

12. z = x² + y², y = x², y = 1, z = 0.

13. (x² + y² + z²)² = az(x² + y²). 14. (x² + y²)² + z⁴ = a³z.

15. (x² + y² + z²)² = a²(x² + y² – z²).

Э7.

Определить центр тяжести тел, ограниченных поверхностями :

1. x² = 2pz, y² = 2px, x = p/2, z = 0. 2. , z = c.

3. Определить центр тяжести контура сферического треугольника: x² + y²+ z² = a², x  0, y  0, z  0.

Вычислить:

4. . 5. , a, b, n > 0.

6. Используя формулу Стирлинга, вычислить: .

Вычислить интегралы:

7. .

8. .

9. .

Вычислить следующие m-кратные интегралы по области D:

10. ,

где D = {x₁ + + x_m  1, x_i  0, i = 1 … m}.

11. , где D = { + +  1}.

12. , где D = { + +  a², –n/2  x_m  n/2}.

13. Вычислить объем m-мерной пирамиды: , x_i  0, a_i > 0, i = 1, 2, … m.

Написать уравнение касательной плоскости к поверхности:

14. ху² + z² = 8 в точке (1, 2, 2).

15. =1 в точке (x₀, y₀, z₀).

Э8.

1. х² + у² = z² в точке (x₀, y₀, z₀).

2. Составить уравнение касательной плоскости и нормали к поверхности: x = 2u – v, y = u² + v², z = u³ – v³ в точке M (3, 5, 7), если (u, v)R².

3. К поверхности xyz = 1 провести касательную плоскость параллельную плоскости x + y + z – a = 0, a = const.

По заданному дифференциалу функции найти функцию (первообразную):

4. dz = (x² + 2xy – y²)dx + (x² – 2xy – y²)dy.

5. .

6. .

7. .

8. .

Вычислить:

9. .

10. – вдоль путей, не проходящих через начало координат.

11. , где С: x = asin2t,

y = 2acostsint, z = acos²t, 0  t  .

12. , где С: х² + у² = а².

13. .

14. , где С – окружность х² + у² = ах.

15. , где С: x = acost, y = acos2t, z = acos3t.

Э9.

1. , где С: x² + y² = a².

2. вдоль путей, не пересекающих прямую у = х.

3. , где С – коническая винтовая линия: x = t cos t, y = t sin t, z = t; (0  t  t₀).

4. Применить формулу Остроградского:

.

5. Вычислить: , где S часть поверхности z = x² + y², отсекаемая плоскостью z = 1.

6. Преобразовать интеграл по поверхности в интеграл по объему:

.

Вычислить интегралы:

7. , где S – граница тела x + y + z  1, x  0, y  0, z  0.

8. , где S: x² + y² + z²  a², z  0.

9. . 10. . 11. , где S: x² + y² = x + y.

12. Вычислить площадь поверхности тора.

13. Найти потенциал поля, если оно потенциально:

.

Найти векторные линии поля:

14. .

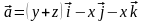15. .

Э10.

1. Найти производную скалярного поля U = x³ – 2x²y + xy² + 1 в точке М(1, 2) в направлении вектора , где N(4, 6).

2. Найти градиент скалярного поля: .

3. Вычислить: .

4. Найти поток вектора через границу тела (шара)

x² + y² + z²  1, заключенной в первом октанте.

5. Найти поток вектора через замкнутую поверхность S, окружающую начало координат.

6. Вычислить поток ротора поля через поверхность параболоида вращения z = 2(1 – x² – y²), отсеченную плоскостью z = 0.

Используя оператор , найти:

7. и , если , – постоянный вектор.

8. и , если . 144. .

9. . 10. , – постоянный вектор.

11. . 12. .

13. и , если , – постоянный вектор.

Вычислить:

14. grad(r). 15. .

Э11.

1. . 2. . 3. .

4. Вычислить div и rot поля , – постоянные векторы.

5. . 6. .

7. , , – постоянный вектор.

8. . 9. .

10. Вычислить div и rot поля , – постоянный вектор.

11. Вычислить div и rot поля , – постоянный вектор.

12. Преобразовать в интеграл по поверхности: , .

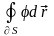Преобразовать в интеграл по объему:

13. . 14. .

15. Вычислить , – постоянная величина, – орт нормали к поверхности S.