
II СЕМЕСТР
Контрольная работа № 21.
Сходимость рядов.
Исследовать на сходимость следующие ряды
1.

2.
2.

3.

4.
4.

5.

6.
6.

7.

8.
8.

9.

10.
10.

11.

12.
12.

13.
13.
 .
.
Контрольная работа № 22.
Определенный интеграл.
Решить следующие задачи
1.
Найти работу, затраченную на возведение
пирамиды Хеопса ( –заданы).
–заданы).
2.
Найти кинетическую энергию тонкого
диска, вращающегося вокруг своего
диаметра ( –заданы).
–заданы).
3. Найти потенциальную энергию стоящего на своем основании конуса ( –заданы).
4.
Найти кинетическую энергию тонкой
эллиптической пластинки, закрученной
вокруг своей большой оси ( –заданы).
–заданы).
5.
Найти работу, необходимую для выкачивания
воды из резервуара формы половины
цилиндра, лежащего на своей боковой
поверхности ( –заданы).
–заданы).
6.
Найти кинетическую энергию конической
поверхности, вращающейся вокруг своей
оси ( –заданы).
–заданы).
7.
Найти работу, необходимую для выкачивания
воды из котла формы параболоида вращения
(радиус крышки
 и глубина
и глубина
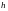 –заданы).
–заданы).
8. Найти кинетическую энергию сферы, вращающейся вокруг своего диаметра( –заданы).
9.
Найти потенциальную энергию конической
поверхности, опирающейся на вершину
( –заданы).
–заданы).
10.
Найти кинетическую энергию тонкого
прямоугольного треугольника, вращающегося
вокруг катета ( –заданы).
–заданы).
11 Найти работу, необходимую для выкачивания воды из полусферического резервуара радиуса .
12. Найти кинетическую энергию конуса, вращающегося вокруг своей оси ( –заданы).
13.
Найти работу, необходимую для поднятия
грунта из конической ямы глубиной
и верхним радиусом
( –задано).
–задано).
Контрольная работа № 23.
Несобственные интегралы 1.
При каких значениях параметров сходятся следующие интегралы
1.

2.
2.

3.

4.
4.

5.

6.
6.

7.

8.
8.

9.

10.
10.

11.

12.
12.

13.
 .
.
Контрольная работа № 24.
Несобственные интегралы 2.
При каких значениях параметров сходятся следующие интегралы
1.

2.
2.

3.
3.

4.
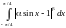
5 .
5 .

6.
6.

7.

8.
8.

9.
9.

10.

11.
11.
12.
13.
13.
 .
.
Контрольная работа № 25.
Дифференциал функции.
Найти дифференциалы следующих функций
1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.
12.

13.
 .
.
Контрольная работа № 26.
Простейшие дифференциальные уравнения
в частных производных.
Решить
следующие простейшие дифференциальные
уравнения относительно функции трех
переменных

1.

2.
2.
3.

4.
4.

5.

6.
6.

7.

8.
8.

9.

10.
10.

11.

12.
12.

13.
 .
.
Контрольная работа № 27.
Дифференцирование неявных функций.
Найти указанные производные функций, заданных неявно
1.
 Найти
Найти
 ;
;
2.
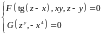 Найти
Найти
 ;
;
3.
 Найти
Найти
 ;
;
4.
 Найти
Найти
 ;
;
5.
 Найти
;
Найти
;
6.
 Найти
Найти
 ;
;
7.
 Найти
;
Найти
;
8.
 Найти
;
Найти
;
9.
 Найти
;
Найти
;
10.
 Найти
;
Найти
;
11.
 Найти
;
Найти
;
12.
 Найти
;
Найти
;
13.
 Найти
;
Найти
;
Контрольная работа № 28.
Замена переменных в дифференциальных выражениях.
Сделать указанную замену переменных и решить получившиеся дифференциальные уравнения:
1.
 ,
,
 ,
,
 ;
;
2.
 ,
,
 ,
,
 ;
;
3.
 ,
,
 ,
,
 ;
;
4.
 ,
,
 ,
,
 ;
;
5.
 ,
,
 ,
,
 ;
;
6.
 ,
,
 ,
,
 ;
;
7.
 ,
,
 ,
,
 ;
;
8.
 ,
,
 ,
,
 ;
;
9.
 ,
,
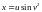 ,
,
 ;
;
10.
 ,
,
 ,
,
 ;
;
11.
 ,
,
 ,
,
 ;
;
12.
 ,
,
 ,
,
 ;
;
13.
 ,
,
 ,
,
 .
.
Контрольная работа № 29.
Экстремумы функций многих переменных.
Исследовать на экстремум следующие функции:
1.
 ;
;
2.
 ;
;
3.
 ;
;
4.
 ;
;
5.
 ;
;
6.
 ;
;
7.
 ;
;
8.
 ;
;
9.
 ;
;
10.
 ;
;
11.
 ;
;
12.
 ;
;
13.
 .
.
Контрольная работа № 30.
Двойные интегралы.
Изменить порядок интегрирования в следующих повторных интегралах:
1.
 ;
2.
;
2.
 ;
;
3.
 ;
4.
;
4.
 ;
;
5.
 ;
6.
;
6.
 ;
;
7.
 ;
8.
;
8.
 ;
;
9.
 ;
10.
;
10.
 ;
;
11.
 ;
12.
;
12.
 ;
;
13.
 .
.
Контрольная работа № 31.
Тройные интегралы.
1.
Найти массу тела
 плотности
плотности
 ,
если:
,
если:
 ;
;
2.
Найти статический момент тела
плотности
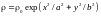 относительно плоскости
относительно плоскости
 :
:
 ;
;
3.
Найти статический момент тела
относительно плоскости
 , если его плотность равна
, если его плотность равна
 и
и
 ;
;
4.
Найти кинетическую энергию вращения
тела
вокруг оси
 , если его плотность равна
, если его плотность равна
 и
и
 ;
;
5.
Найти массу тела
плотности
 ,
если:
,
если:
 ;
;
6.
Найти кинетическую энергию вращения
тела
вокруг оси
 , если его плотность равна
, если его плотность равна
 и
и
 ;
;
7.
Найти статический момент тела
относительно плоскости
 , если его плотность равна
, если его плотность равна
 и
и
 ;
;
8.
Найти массу тела
плотности
 ,
если:
,
если:
 ;
;
9.
Найти статический момент тела
относительно плоскости
, если его плотность равна
 и
и
 ;
;
10.
Найти кинетическую энергию вращения
тела
вокруг оси
 ;
;
11.
Найти массу тела
плотности
 ,
если:
,
если:
 ;
;
12.
Найти кинетическую энергию вращения
тела
вокруг оси
 , если его плотность равна
, если его плотность равна
 и
и
 ;
;
13.
Найти статический момент тела
относительно плоскости
, если его плотность равна
 и
и
 ;
;
Контрольная работа № 32. Криволинейные интегралы.
Вычислить указанные криволинейные интегралы второго рода вдоль заданного контура С:
1.
 ;
;
 ;
;
 ;
;
2.
 ;
;
 ;
;
;
3.
 ;
;
 ;
;
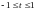 ;
;
4.
 ;
;
 ;
;
 ;
;
5.
 ;
;
 ;
;
 ;
;
, если его плотность равна
 и
и
6.
 ;
;
 ;
;
 ;
7.
;
7.
 ;
;
 ;
;
 ;
;
8.
 ;
;
 ;
;
 ;
;
9.
 ;
;
 ;
;
;
10.
 ;
;
 ;
;
;
11.
 ;
;
 ;
;
 ;
;
12.
 ;
;
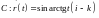 ;
;
;
13.
 ;
;
 ;
;
.
Контрольная работа № 33.
Поверхностные интегралы.
Найти поток векторного поля через поверхность :
1.
 ;
;
 ;
;
2.
 ;
;
 ;
;
3.
 ;
;
 ;
;
4.
 ;
;
 ;
;
5.
 ;
;
 ;
;
6.
 ;
;
 ;
;
7.
 ;
;
 ;
;
8.
 ;
;
 ;
;
9.
;
 ;
;
10.
 ;
;
 ;
;
11.
 ;
;
;
;
12.
 ;
;
 ;
;
13.
 ;
;
 .
.
Контрольная работа № 34.
Элементы теории поля.
Какие из приведенных ниже формул справедливы:
Вариант 1 Вариант 2 Вариант 3
1.
 ;
;
 ;
;
 ;
;
2.
 ;
;
 ;
;
 ;
;
3.
 ;
;
 ;
;
 ;
;
4.
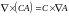 ;
;
 ;
;
 ;
;
5.
 ;
;
 ;
;
 ;
;
6.
 ;
;
 ;
;
 ;
;
7.
 ;
;
 ;
;
 ;
;
8.
 ;
;
 ;
;
 ;
;
9.
 ;
;
 ;
;
 .
.
В приведенных равенствах считается, что:
 –
постоянные скаляры;
–
постоянные скаляры;
 –
скалярные поля;
–
скалярные поля;
 –
постоянний вектор;
–
постоянний вектор;
 –
векторные поля;
–
векторные поля;
 –
контур;
–
контур;
 –
поверхность и объем;
–
поверхность и объем;
 –
их границы.
–
их границы.
