Пример решения задачи

Постановка задачи. Завод ЖБК планирует выпуск двух новых изделий. Оба изделия имеют одинаковые качественные характеристики, но 1-ое приносит заводу 5, а 2-е 6 условные единиц прибыли. Определить какое количество изделий 1-го и 2-го типа должен выпустить завод ЖБК, чтобы получить максимальную прибыль при заданном объеме трудовых затрат и материальных ресурсов.

Описание задачи. Обозначим:

Х₁ – количество изделий 1-го типа;

Х₂ - количество изделий 2-го типа;

a_ij – норма расхода сырья на одно изделие;

b_i – наличие ресурсов;

П_мах – максимальная прибыль;

- количество вариантов изделий; j = 2;

- количество ресурсов; i = 4.

Целевая функция 5Х₁ + 6Х₂ = П_мах,

Ограничения a₁₁ Х₁ + a₁₂ Х₂ ≤ b₁;

a₂₁ Х₁ + a₂₂ Х₂ ≤ b₂;

a₃₁ Х₁ + a₃₂ Х₂ ≤ b₃;

a₄₁ Х₁ + a₄₂ Х₂ ≤ b₄.

Значение a_ij и b_i приведены в табл. 1.

Таблица 1

Наименование материалов	Ед. изм.	Расход на 1 изделие по вариантам		Наличие ресурсов
		1	2
Цемент	т	0,3	0,2	1 тыс.т
Сталь	т	0,1	0,2	0,6 тыс.т
Щебень	м3	0,3	0,3	1,5 тыс. м3
Трудозатраты	чел./день	0,1	0,1	0,6 тыс. чел./день

Заменяя неравенства равенствами, составляем систему управлений с конкретными коэффициентами при Х₁ и Х₂.

0,3 Х₁ + 0,2 Х₂ = 1;

0,1 Х₁ + 0,2 Х₂ = 0,6;

0,3 Х₁ +0,3 Х₂ = 1,5;

0,1 Х₁ + 0,1 Х₂ = 0,8.

Из анализа системы линейных уравнений видно, что она состоит из 4-х уровней с 2-мя неизвестными. Это значит, что система имеет множество решений. Такого типа задачи решаются либо на ЭВМ, либо геометрически. При этом, заменяя неравенства равенствами и решая каждое уравнение отдельно как уравнение прямой на плоскости, находим совокупность этих прямых:

0,3 Х₁ + 0,2 Х₂ = 1,0.

Примем Х₁ = 0, тогда Х₂ = при Х₂ = 0 получим Х₁ =

Подобным образом находим все значения Х₁ и Х₂ для остальных уравнений. Отложим значения Х₁ и Х₂ на осях координат и соединим их прямыми. В результате получилась совокупность пересекающихся прямых (рисунок).

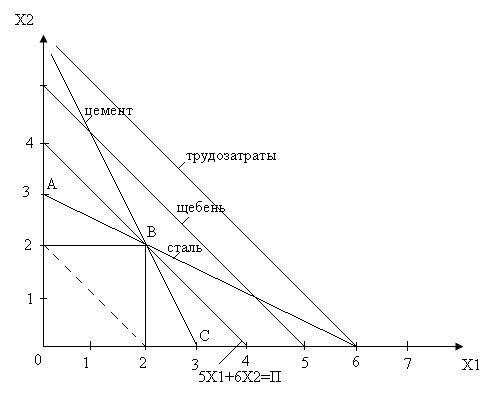
Выделим поверхность ОАВС, представляющую ту область, в каждой точке которой одновременно удовлетворяются все четыре неравенства. Но нас интересуют такие значения Х₁ и Х₂, при которых будет получена максимальная прибыль.

Из уравнения целевой функции 5Х₁ + 6Х₂ = П_мах, задавшись величиной П = 1, находим Х₁ и Х₂: при Х₁ = 0 Х₂ = , при Х₂ = 0 Х₁ = .

Построим прямую на плоскости. В дальнейшем параллельно этой прямой построим прямую, касательную сгибающей. Координаты точки касания и будут отвечать требованиям, поставленным в задаче, т.е. получению максимальной прибыли. Этим условиям удовлетворяет точка с координатами Х₁ = 2, Х₂ = 2. Таким образом, оптимальный план будет при 2 тыс. изделий 1-го типа и 2 тыс. изделий 2-го типа. Этот план принесет заводу прибыль.

П = 5*2000+6*2000 = 22 тыс. условных единиц.

Задание студенту

1. По исходным данным из табл. 2 составить систему уравнений (ограничений и целевую функцию) для решения задачи на ЭВМ или геометрическим методом.

2. Решить задачу геометрическим методом.

Условие задачи

Определить максимальное количество квадратных метров жилья, которое может возвести строительная организация в домах 2-х типов при наличии определенных ресурсов:

Х₁ – количество жилья в домах 1-го типа, м²;

Х₂ – то же, в домах 2-го типа;

a_ij – норма расхода ресурсов на 1 м² жилой площади;

b_i – наличие ресурсов: j = 2; i = 6.

Контрольная работа №5

МЕЖОТРАСЛЕВЫЕ СВЯЗИ СТРОИТЕЛЬСТВА

Строительство связано с многочисленными отраслями промышленности, транспортом, сельским хозяйством, так как выступает и как производители строительной продукции и как потребитель продукции и услуг других отраслей материального производства. В настоящее время 75% производственного потребления предметов труда в строительстве удовлетворяются за счет трех крупных комплексных отраслей промышленности: строительных материалов, металлургии, лесной и деревообрабатывающей промышленности. В планах промышленного производства и строительства для расчетов пропорциональности в развитии отдельных отраслей и их материально-технического обеспечения используется метод балансов.

Составлением межотраслевых балансов достигается наиболее полное отражение экономических связей в народном хозяйстве. Межотраслевые связи строительства – часть балансов народного хозяйства. Для расчета межотраслевого баланса используются математические методы и электронно-вычислительная техника.