4. Критерий Гурвица.

Формулировка критерия Гурвица для непрерывных систем справедлива и для дискретных систем, если в характеристическом уравнении системы произвести замену

w - преобразование.

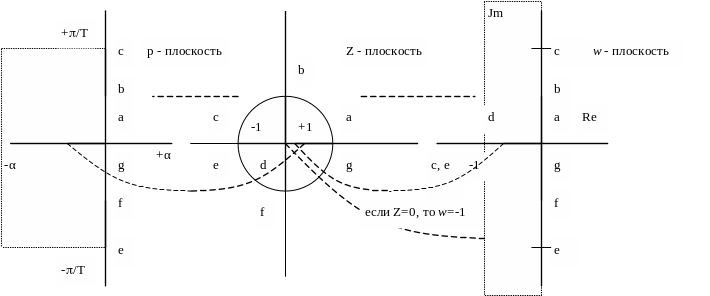
Введем комплексную переменную w, связанную с комплексной переменной z билинейным преобразованием :

, где ;

.

При изменении частоты в пределах псевдочастота Ω пробегает все значения от - до +, а комплексная переменная w движется по оси мнимых чисел от -j до +j. Внутренняя часть круга единичного радиуса отображается при этом на левую полуплоскость.

При помощи w - преобразования осуществляется конформное отображение внутренности окружности единичного радиуса на плоскости z в левую полуплоскость w. При этом контур окружности единичного радиуса переходит в мнимую ось плоскости w.

При исследовании дискретных систем по преобразованным при помощи w - преобразования передаточным функциям могут использоваться обычные приемы и критерии, справедливые для непрерывных систем, в том числе и критерий Гурвица.

55. Методы построения лпчх исходных (нескорректированных) цифровых систем. Учёт постоянного временного запаздывания в сау с цвм. Построение лпчх исходной (нескорректированной) цифровой сау

Для построения ЛПЧХ исходной ЦАС определяют дискретную передаточную функцию разомкнутой системы, затем путем подстановки

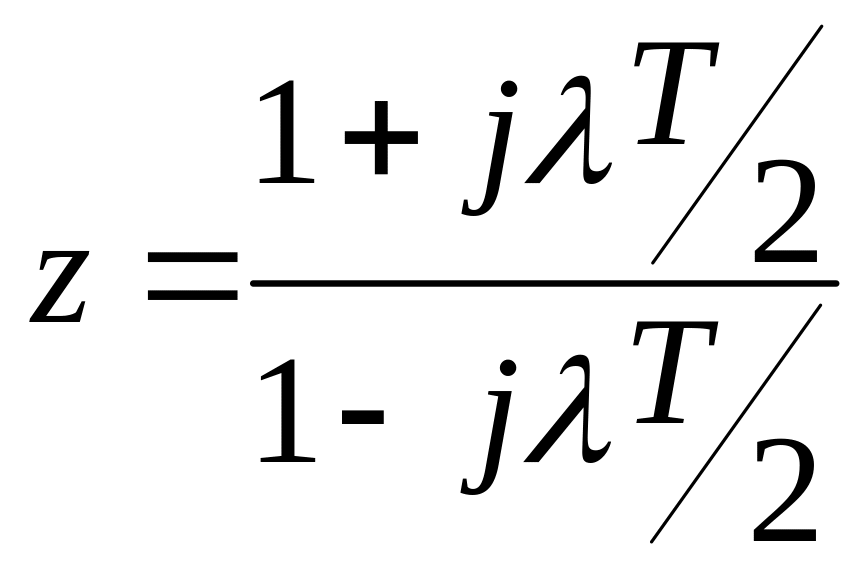
получают дискретную частотную передаточную функцию разомкнутой цифровой системы. Порядок построения ЛЧХ цифровых систем по дискретным частотным передаточным функциям такой же, как и для непрерывных систем.

Такой путь определения ЛПЧХ, как правило, ведет к громоздким и трудоемким построениям и промежуточным вычислениям, что связано с утратой основного достоинства метода – простоты и наглядности использования ЛЧХ.

Поэтому построение ЛПЧХ исходной ЦАС проводят обычно приближенными способами. Применимость этих способов зависит от вида передаточных функций непрерывной части САУ правее частоты , наличия колебательных, консервативных и неминимально-фазовых звеньев, а также расположения их сопрягающих и резонансных частот относительно частоты , порядка экстраполятора и вида . Обычно используют или метод ограничений, или метод упрощенного расчета дискретной ЛЧХ в области высоких частот.

Л

jω

JmZi

ПЧХ целесообразно строить раздельно для области низких частот ( ) и для области высоких частот ( ).

ReZi

В методе ограничений в области низких частот (левее частоты ) ЛЧХ дискретной частотной передаточной функции совпадает с ЛЧХ непрерывной части ЦАС, если , а передаточные коэффициенты преобразователей приведены к передаточной функции непрерывной части системы.

Если передаточная функция непрерывной части имеет вид

,

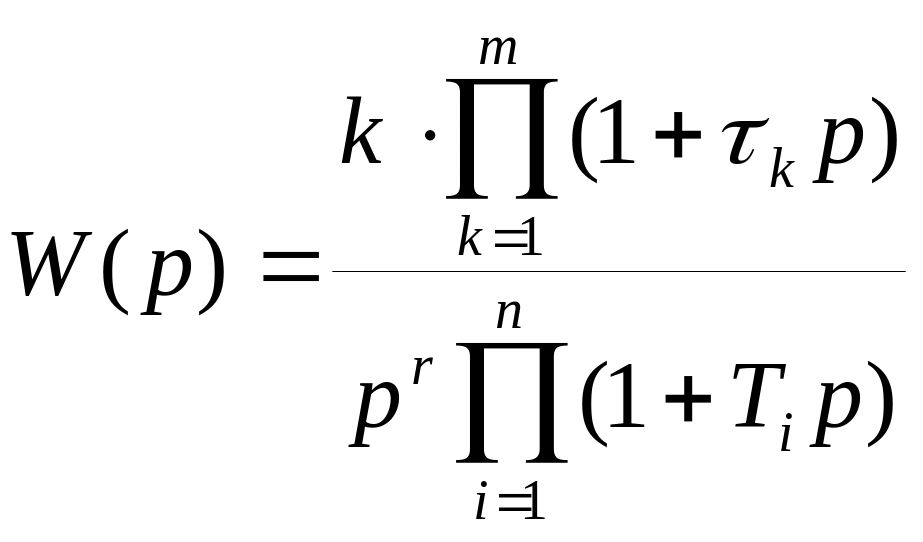где постоянные времени делятся на две группы : к первой группе ( , , …, ) отнесем те из них, которым соответствуют сопрягающие частоты меньше (большие постоянные времени), они участвуют в формировании низкочастотной части логарифмических характеристик; ко второй группе ( , , …, ) отнесем постоянные времени, которым соответствуют сопрягающие частоты больше чем (малые постоянные времени). Постоянным времени , , …, соответствуют сопрягающие частоты, меньшие частоты , то при пересечении ЛАЧХ исходной САУ вертикальной прямой асимптотой с наклоном –20 дБ/дек дискретная частотная передаточная функция имеет вид

,

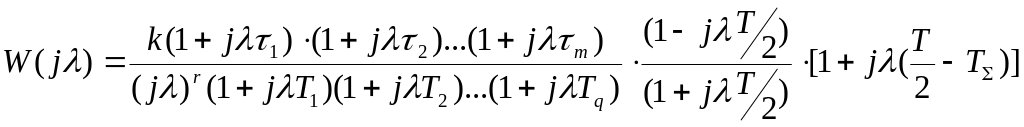где ;

при пересечении вертикальной линии асимптотической ЛАЧХ непрерывной части системы с наклоном –40 дБ/дек

.

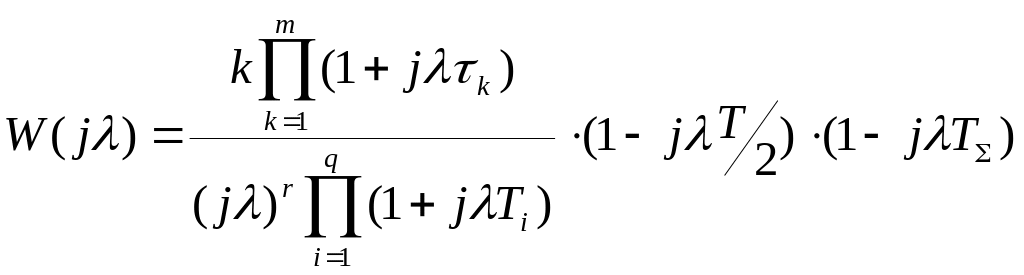Метод упрощенного расчета используют, например, когда в области частот передаточную функцию непрерывной части исходной системы можно аппроксимировать выражением, для которого либо известна , либо может быть легко определена.

Например, если , где ,

- частота, определяемая точкой пересечения асимптоты, имеющей наклон –60 дБ/дек с осью абсцисс (эта асимптота проходит через точку сопряжения с низкочастотной частью ЛАЧХ на линии ), то построение псевдочастотной ЛЧХ производится по дискретной частотной передаточной функции :

.
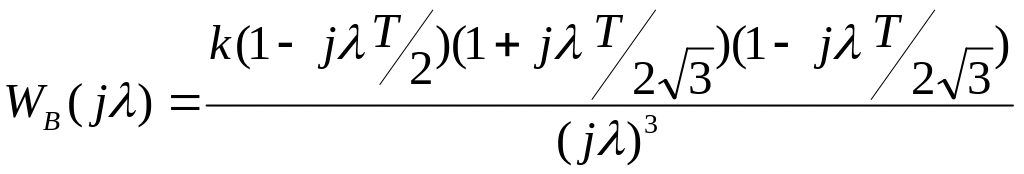