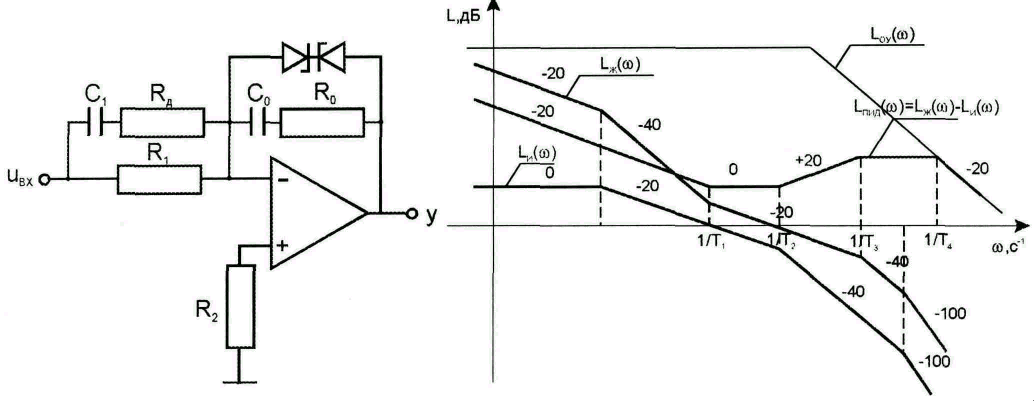
Реализация пид-регулятора

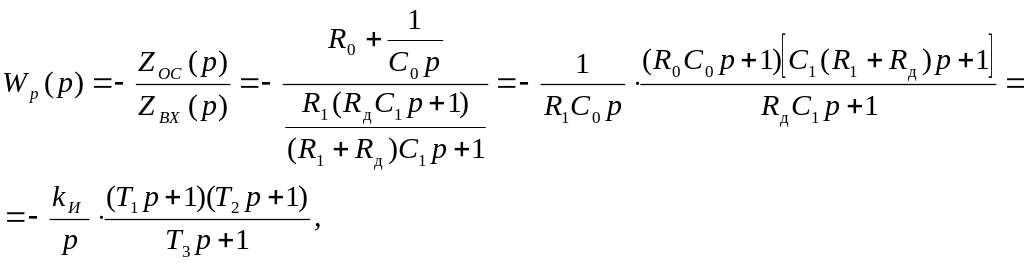
где , , , , причем .

По ЛАЧХ операционного усилителя определяем . Тогда передаточная функция реального регулятора имеет вид .

В системах чаще всего применяется ПИД-регулятор.

49. Расчёт систем комбинированного управления: расчёт компенсирующих устройств по каналу возмущения.

Пусть структурная схема исходной системы преобразована к виду, изображенному на рис.1.

Перенесем на вход системы точку приложения возмущения (рис. 2).

y₁

y₁+u-y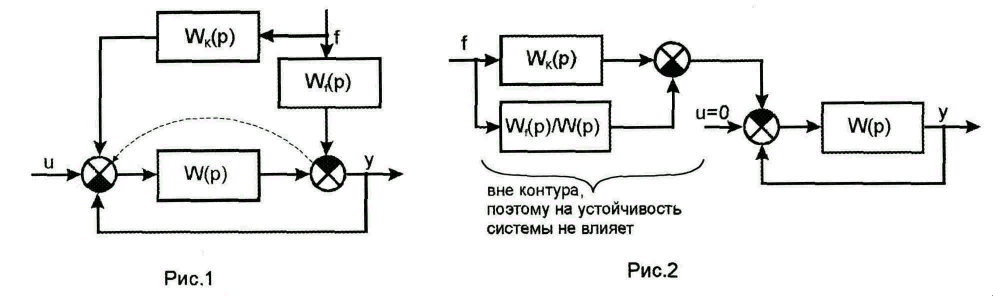

Запишем уравнение для выходной координаты:

.

Влияние на выходную функцию со стороны возмущения f будет отсутствовать, если выполняется условие абсолютной инвариантности системы к возмущающему воздействию:

- условие полной компенсации возмущения.

Внешние регуляторы используются для получения инвариантности по каналу возмущения с точностью до .

Пример. Пусть объект и регулятор ведут себя как апериодические звенья. Наибольшая постоянная времени, как правило, принадлежит объекту.

Тогда

, , ,

, .

Г

1/Т₀

1/Тp

рафики на рис. 3.

Компенсирующая цепь должна обладать дифференцирующими свойствами, причем активными дифференцирующими свойствами на высоких частотах (так как характеристика отчасти располагается выше оси частот).

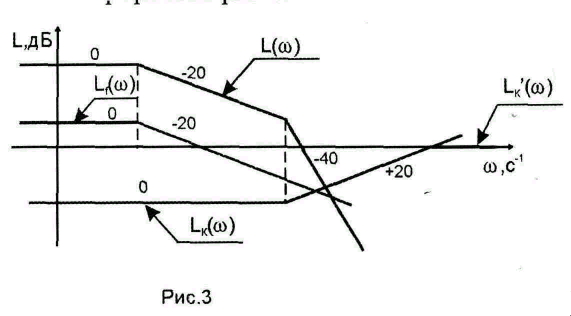Достижение абсолютной инвариантности невозможно, однако эффект компенсации может быть значительным даже при простой компенсирующей цепи, обеспечивающей реализацию в ограниченном диапазоне частот ( на рис. 3).

Технически трудно и не всегда возможно измерить возмущение, поэтому при проектировании систем часто используют косвенные методы измерения возмущающих воздействий.

50. Расчёт систем комбинированного управления: расчёт систем с компенсацией динамической ошибки по каналу управления.

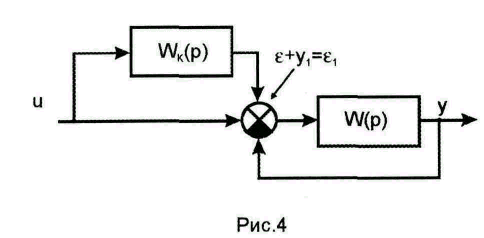
Для этой системы, структурная схема которой изображена на рис. 4, справедливы следующие соотношения:

;

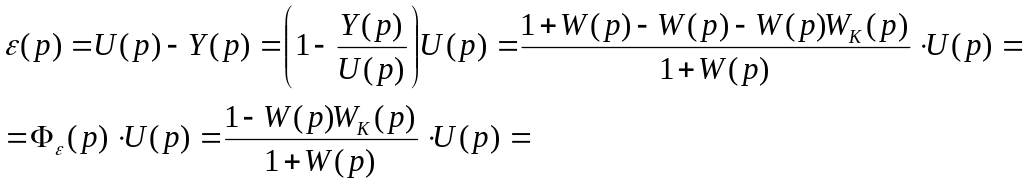
= – передаточная функция по сигналу ошибки.

Можем добиться условия полной компенсации ошибки, если выбрать компенсирующую цепь с параметрами:

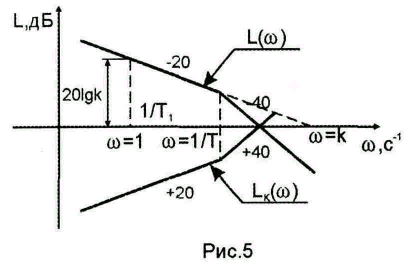
(1) – условие абсолютной инвариантности системы к ошибке по каналу управления.

Передаточная функция системы с компенсирующей цепью .

В этом случае ,

.

Следящие системы реализуются астатическими. Рассмотрим пример для таких систем (рис.5).

В области высоких частот дифференцирование второго порядка в компенсирующей цепи приводит к насыщению усилителей и размыканию цепи при высоком уровне помех. Поэтому осуществляется приближенная реализация, которая дает ощутимый эффект регулирования.

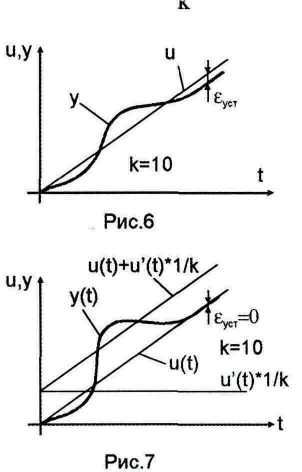
Астатические

системы характеризуются

добротностью

– передаточный

коэффициент k определяется при =1 и =k.

Если k=10, то ошибка в 10%, так как

, система низкого качества (рис.6).

Введем компенсирующую цепь с передаточной функцией

. Такой цепью может служить тахогенератор, если

вход механический. Реализация системы с малой добротностью

проста.

Пусть , из условия (1) получим .

Тогда, имея систему с астатизмом 1-го порядка, получим систему с

астатизмом второго порядка (рис.7).

Всегда Y отстает от управляющего сигнала; введя , уменьшаем ошибку. Компенсирующая цепь не влияет на устойчивость.

Как правило, компенсирующее звено должно обладать дифференцирующими свойствами и реализовываться с использованием активных элементов. Точное выполнение условия абсолютной инвариантности невозможно в виду технической нецелесообразности получения производной выше второго порядка (в контур регулирования вводится высокий уровень помех, возрастает сложность компенсирующего устройства) и инерционности реальных технических устройств. Количество апериодических звеньев в компенсирующем устройстве проектируют равным числу элементарных дифференцирующих звеньев. Постоянные времени апериодических звеньев рассчитывают по условию работы звеньев в существенной области частот, т.е.

, .