
- •Объекты управления.
- •Обобщенная структурная схема объекта управления
- •Объекты с самовыравниванием:
- •Объекты без самовыравнивания.
- •Объекты с запаздыванием.
- •Типовая структурная схема трёхкоординатной сау.
- •3. Классификация сау.
- •Фундаментальные принципы управления. Принцип управления по возмущению (принцип компенсации, принцип Понселе).
- •1. Принцип разомкнутого управления
- •Принцип управления по возмущению (принцип компенсации, принцип Понселе).
- •5. Фундаментальные принципы управления. Принцип обратной связи (принцип управления по отклонению контролируемой функции от входного воздействия, принцип Ползунова-Уатта).
- •6. Принцип обратной связи.
- •7. Фундаментальные принципы управления. Комбинированный принцип управления.
- •8. Статические и астатические сау.
- •9. Статические характеристики звеньев и объектов сау. Динамические характеристики систем управления.
- •Математическое описание сау.
- •11. Типовые входные воздействия.
- •12. Частотные характеристики объектов и систем управления.
- •13. Типовые динамические звенья сау: безынерционное звено, апериодическое звено 1-го порядка.
- •14. Инерционное звено 2-го порядка.
- •15. Логарифмические частотные характеристики колебательного звена.
- •20. Уравнение статики и уравнение динамики сау.
- •21. Критерий устойчивости Гурвица.
- •22. Методика анализа устойчивости сау.
- •23. Передаточные функции систем различной структуры.
- •Последовательное соединение звеньев.
- •Параллельное включение звеньев.
- •Встречно-параллельное соединение динамических звеньев.
- •3.2. Контур с положительной обратной связью.
- •24. Преобразование структурных схем.
- •25. Теоремы а.М. Ляпунова, определение критерия устойчивости, необходимое условие устойчивости Рауса, формулировка критерия устойчивости Гурвица. Теоремы а.М. Ляпунова.
- •Критерии устойчивости сау.
- •26. Методика построения логарифмической частотной характеристики сау: статические системы.
- •27. Передаточные и переходные функции сау.
- •28. Методика построения логарифмической частотной характеристики сау: астатические системы.
- •29. Принцип аргумента.
- •30. Критерий устойчивости Найквиста для систем с неустойчивой разомкнутой цепью.
- •3 1. Анализ качества сау в статике.
- •32. Методика построения логарифмической частотной характеристики контура с отрицательной обратной связью.
- •33. Критерий Найквиста, сформулированный я.З.Цыпкиным. Формулировка критерия Найквиста для лчх. Формулировка я.З. Цыпкина
- •Критерий Найквиста для лчх
- •34. Критерий Найквиста: причины широкого применения в инженерной практике, критерий Найквиста для систем, устойчивых в разомкнутом состоянии.
- •1. Система, устойчивая в разомкнутом состоянии
- •35. Методика построения логарифмической частотной характеристики сау: параллельное соединение звеньев.
- •36. Анализ качества сау в динамике.
- •Прямые показатели качества сау
- •37. Запасы устойчивости. Запасы устойчивости
- •38. Анализ качества сау. Исследование качества сау
- •Методы исследования качества сау
- •39. Критерий Найквиста для систем, разомкнутые цепи которых кроме полюсов с отрицательными вещественными частями имеют полюса на мнимой оси.
- •40. Критерий Найквиста для систем, разомкнутая цепь которых устойчива.
- •Система, устойчивая в разомкнутом состоянии
- •41. Передаточная функция встречно-параллельного соединения звеньев. Правило определения передаточных функций замкнутых сау.
- •3.1. Контур с отрицательной обратной связью.
- •3.2. Контур с положительной обратной связью.
- •42. Расчёт линейных непрерывных сау по заданной точности в установившемся режиме работы.
- •1. Расчет установившегося режима работы сар по заданным коэффициентам рассогласования (ошибки)
- •43. Алгоритм построения желаемой лчх по методу в.В.Солодовникова.
- •44. Синтез корректирующей цепи последовательного типа.
- •45. Приближённый метод построения лчх корректирующей отрицательной обратной связи.
- •46. Типовые регуляторы: пд-регулятор.
- •Реализация пд-регулятора
- •47. Типовые регуляторы: пи-регулятор.
- •Реализация пи-регулятора
- •48. Типовые регуляторы: пид-регулятор.
- •Реализация пид-регулятора
- •49. Расчёт систем комбинированного управления: расчёт компенсирующих устройств по каналу возмущения.
- •50. Расчёт систем комбинированного управления: расчёт систем с компенсацией динамической ошибки по каналу управления.
- •51. Этапы проектирования сау. Схемы включения корректирующих устройств.
- •52. Качество работы цифровых сау. Три типа желаемых лпчх цифровых систем.
- •53. Дискретное преобразование Лапласа. Z-преобразование. Основные свойства и теоремы z-преобразования. Дискретное преобразование Лапласа
- •Основные свойства и теоремы z-преобразования
- •4. Критерий Гурвица.
- •55. Методы построения лпчх исходных (нескорректированных) цифровых систем. Учёт постоянного временного запаздывания в сау с цвм. Построение лпчх исходной (нескорректированной) цифровой сау
- •Учет постоянного временного запаздывания
- •61. Особенности синтеза систем управления с эвм в качестве управляющего устройства.
41. Передаточная функция встречно-параллельного соединения звеньев. Правило определения передаточных функций замкнутых сау.
Встречно-параллельное соединение динамических звеньев.
3.1. Контур с отрицательной обратной связью.

Составим систему уравнений контура
Тогда
передаточная функция контура с отрицательной обратной связью.
Контур с неединичной обратной связью может быть преобразован к контуру с единичной отрицательной обратной связью
где
Эквивалентная структурная
схема контура с ООС.

3.2. Контур с положительной обратной связью.

где

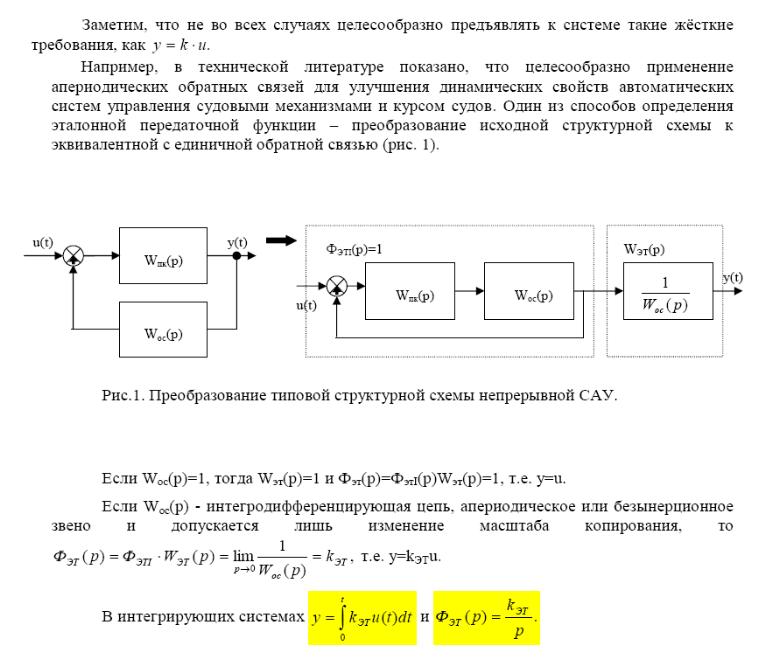
42. Расчёт линейных непрерывных сау по заданной точности в установившемся режиме работы.
Одно из основных требований, которым должна удовлетворять САУ, заключается в обеспечении необходимой точности воспроизведения задающего (управляющего) сигнала в установившемся режиме работы.
Пусть структурная схема САР приведена к виду
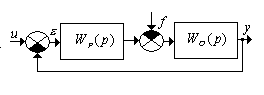
Тогда в
квазиустановившемся режиме работы САР
рассогласование
![]() представимо в виде сходящегося ряда
представимо в виде сходящегося ряда
![]() ,
,
где
![]() выполняют роль весовых констант.
выполняют роль весовых констант.
Очевидно, что такой
процесс может иметь место только в том
случае, если
![]() –медленно
меняющаяся и достаточно плавная функция.
–медленно
меняющаяся и достаточно плавная функция.
Если представить передаточную функцию разомкнутой системы в виде
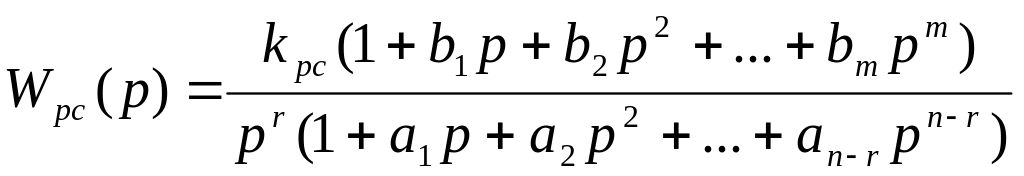 ,
,
то при r=0
![]()
при r=1
![]()
![]()
при r=2
![]()
![]()
при r=3
![]()
![]()
1. Расчет установившегося режима работы сар по заданным коэффициентам рассогласования (ошибки)
Точность работы
системы в установившемся режиме
определяется величиной передаточного
коэффициента разомкнутой системы
![]() ,
который определяется в зависимости от
формы задания требований к точности
системы.
,
который определяется в зависимости от
формы задания требований к точности
системы.
Расчет ведется следующим образом.
СТАТИЧЕСКИЕ САР. Здесь задается величина коэффициента позиционной ошибки
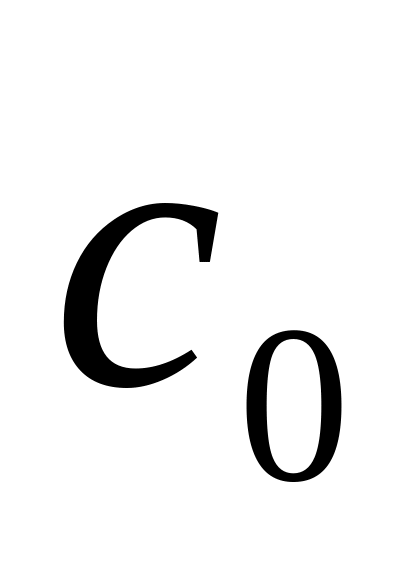 ,
по которому определяется
:
,
по которому определяется
:
 .
.
L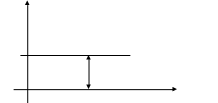 ,
,
дБ
20lgkpc
ω, с-1
АСТАТИЧЕСКИЕ СИСТЕМЫ 1-го порядка.
В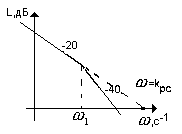 этом случае задан коэффициент
этом случае задан коэффициент
![]() ,
по которому определяется
,
по которому определяется
![]()
Если заданы
коэффициенты
и
![]() ,
то
,
то
![]() ,
который определяет положение низкочастотной
асимптоты ЛАЧХ разомкнутой системы с
наклоном -20 дБ/дек, а вторая асимптота
имеет наклон -40 дБ/дек при сопрягающей
частоте
,
который определяет положение низкочастотной
асимптоты ЛАЧХ разомкнутой системы с
наклоном -20 дБ/дек, а вторая асимптота
имеет наклон -40 дБ/дек при сопрягающей
частоте
![]() (рис.1).
(рис.1).
Рис.1.
АСТАТИЧЕСКИЕ СИСТЕМЫ 2-го порядка.
П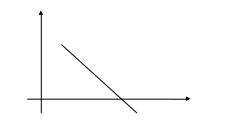 о
заданному коэффициенту
определим kpc:
о
заданному коэффициенту
определим kpc:
![]()
L,
дБ
-40
![]()
ω, с-1
43. Алгоритм построения желаемой лчх по методу в.В.Солодовникова.
Выбор частоты среза Lж(w).
Е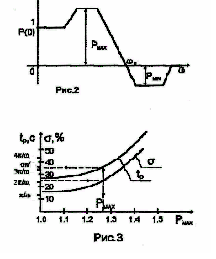 сли
заданы перерегулирование
сли
заданы перерегулирование
![]() и время затухания переходного процесса
и время затухания переходного процесса
![]() ,
то используются номограммы В.В.Солодовникова
или А.В.Фатеева; если задан показатель
колебательности М, то расчет ведут по
методу В.А.Бесекерского.
,
то используются номограммы В.В.Солодовникова
или А.В.Фатеева; если задан показатель
колебательности М, то расчет ведут по
методу В.А.Бесекерского.
В
основу построения номограмм качества
В.В.Солодовниковым положена типовая
вещественная частотная характеристика
замкнутой САУ (рис. 2). Для статических
систем (n=0)
![]() ,
для астатических систем (n=1,
2,…)
,
для астатических систем (n=1,
2,…)
![]() .
.
Этот метод
предполагает, что соблюдается соотношение
![]() .
.
В качестве исходных
приняты показатели качества
и
,
которые связаны с параметрами вещественной
частотной характеристики диаграммой
качества (рис. 3). По заданному
![]() с помощью кривой
с помощью кривой
![]() (рис.3) определяется соответствующее
значение
(рис.3) определяется соответствующее
значение
![]() .
Затем по
и кривой
.
Затем по
и кривой
![]() определяется значение
определяется значение
![]() ,
которое приравнивается заданному
,
получаем
,
которое приравнивается заданному
,
получаем
![]()
![]() ,
где
,
где
![]() – значение частоты среза, при котором
время регулирования не превысит заданного
значения
.
– значение частоты среза, при котором
время регулирования не превысит заданного
значения
.
С другой стороны
ограничивается допустимым ускорением
регулируемой координаты
![]() .
Рекомендовано
.
Рекомендовано
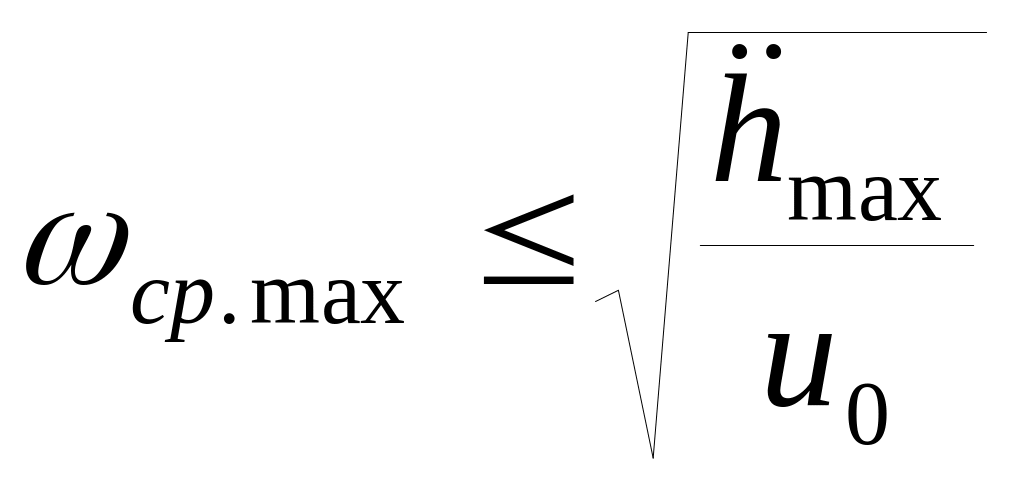 ,
где
,
где
![]() – начальное рассогласование.
– начальное рассогласование.
Время регулирования
можно приближенно определить, используя
эмпирическую формулу
![]() ,
где коэффициент числителя принимается
равным 2 при
,
где коэффициент числителя принимается
равным 2 при
![]() ,
3 при
,
3 при
![]() ,
4 при
,
4 при
![]() .
.
Всегда желательно проектирование системы с максимально возможным быстродействием.
Как правило,
![]() не превышает
не превышает
![]() более, чем на ½ декады. Это связано с
усложнением корректирующих устройств,
необходимостью введения в систему
дифференцирующих звеньев, что уменьшает
надежность и помехоустойчивость, а
также в силу ограничения по максимально
допустимому ускорению регулируемой
координаты.
более, чем на ½ декады. Это связано с
усложнением корректирующих устройств,
необходимостью введения в систему
дифференцирующих звеньев, что уменьшает
надежность и помехоустойчивость, а
также в силу ограничения по максимально
допустимому ускорению регулируемой
координаты.
Частоту среза
![]() можно повышать лишь увеличением
можно повышать лишь увеличением
![]() .
Статическая точность при этом возрастает,
но ухудшаются условия устойчивости.
.
Статическая точность при этом возрастает,
но ухудшаются условия устойчивости.
Принятие решения по выбору должно иметь достаточное обоснование.
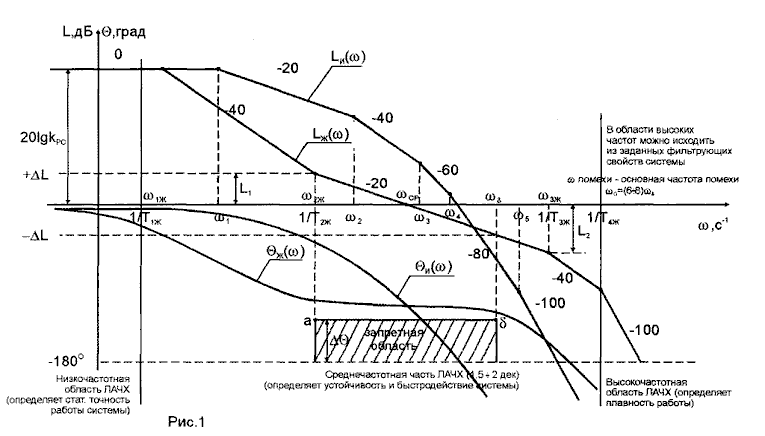
Строим среднечастотную асимптоту. Ее проводим через точку на оси абсцисс с наклоном –20 дБ/дек.
Среднечастотную асимптоту сопрягаем с низкочастотной асимптотой так, чтобы в интервале частот, в котором
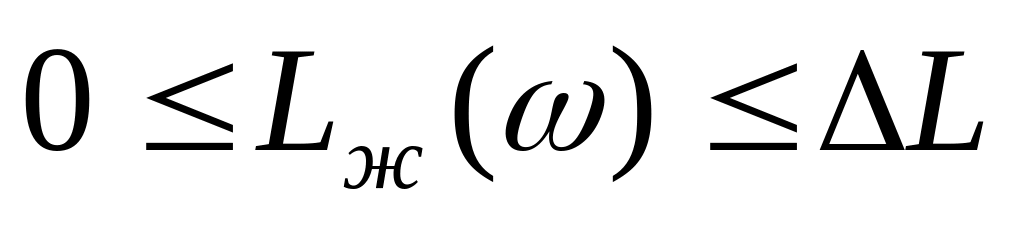 ,
иметь избыток фазы
,
иметь избыток фазы
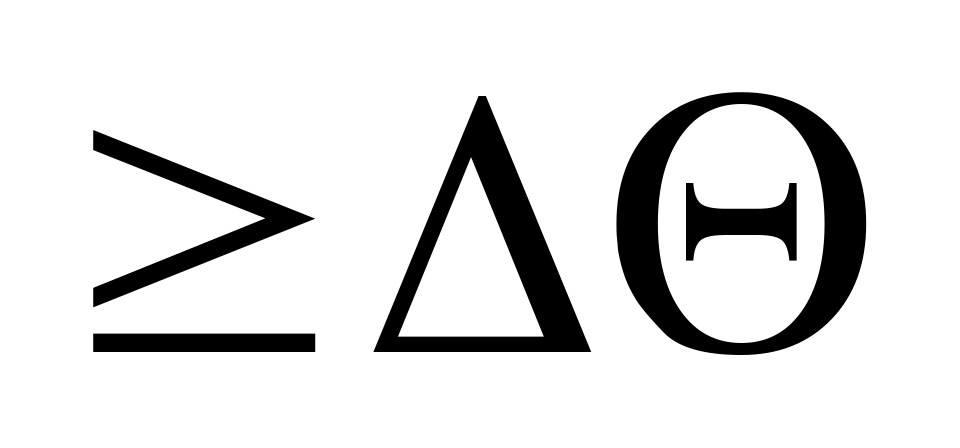 .
Избыток фазы и избыток модуля
.
Избыток фазы и избыток модуля
 определяем по номограмме (рис. 4).
Сопрягающая асимптота имеет наклон
–20, -40 или –60 дБ/дек при n=0
(n
- порядок астатизма системы); -40, -60 дБ/дек
при n=1
и -60 дБ/дек при n=2.
определяем по номограмме (рис. 4).
Сопрягающая асимптота имеет наклон
–20, -40 или –60 дБ/дек при n=0
(n
- порядок астатизма системы); -40, -60 дБ/дек
при n=1
и -60 дБ/дек при n=2.
∆L, дБ
∆θ, град
Е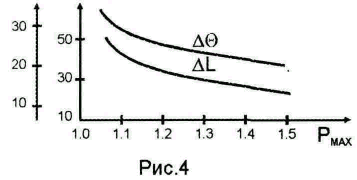 сли
избыток фазы
сли
избыток фазы
![]() окажется меньше
окажется меньше
![]() ,
то сопрягающую асимптоту следует
сместить влево или уменьшить ее наклон.
Если избыток фазы больше допустимого,
то сопрягающую асимптоту смещают вправо
или увеличивают ее наклон.
,
то сопрягающую асимптоту следует
сместить влево или уменьшить ее наклон.
Если избыток фазы больше допустимого,
то сопрягающую асимптоту смещают вправо
или увеличивают ее наклон.
Первоначальная
сопрягающая частота определяется из
выражения
![]() .
.
Рекомендуемая
разность
![]() должна составлять несколько градусов.
Однако, часто (в статических системах)
должна составлять несколько градусов.
Однако, часто (в статических системах)
![]() значительно превосходит
,
и уменьшение
затруднительно. В этом случае принимается
.
значительно превосходит
,
и уменьшение
затруднительно. В этом случае принимается
.
Среднечастотную асимптоту сопрягаем с высокочастотной частью
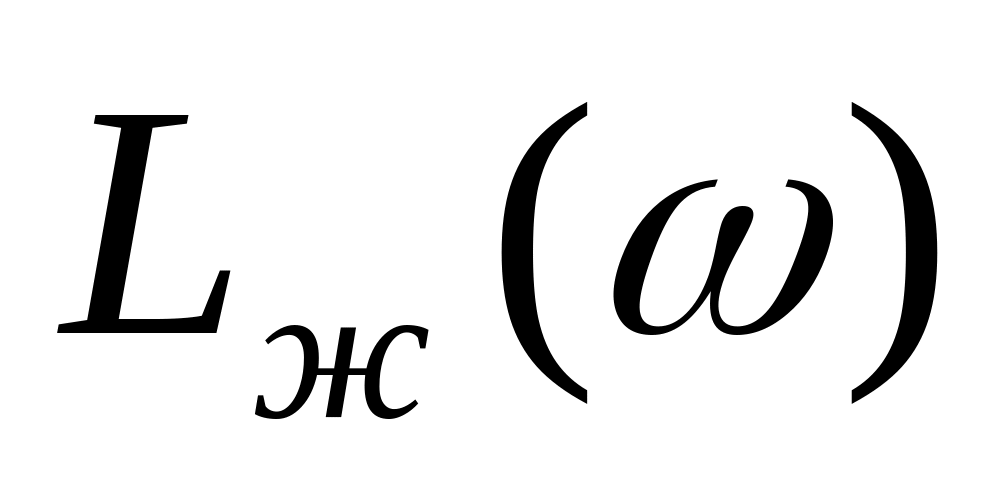 таким образом, чтобы в интервале частот,
где
таким образом, чтобы в интервале частот,
где
 ,
избыток фазы был
.
Сопрягающую частоту определяем по
соотношению
,
избыток фазы был
.
Сопрягающую частоту определяем по
соотношению
 .
.
Если на сопрягающей частоте < , то сопрягающую асимптоту смещают вправо или уменьшают ее наклон.
Если
>
,
то сопрягающую асимптоту смещают влево
или увеличивают ее наклон. Рекомендуемая
разность
![]() должна составлять несколько градусов.
Правая сопрягающая частота сопрягающей
асимптоты
должна составлять несколько градусов.
Правая сопрягающая частота сопрягающей
асимптоты
![]() .
.
Как правило, наклон
этой асимптоты составляет -40 дБ/дек, а
допустимая разность
![]() .
Проверка производится на частоте, при
которой
.
Проверка производится на частоте, при
которой
![]() .
.
Высокочастотная часть проектируется параллельно
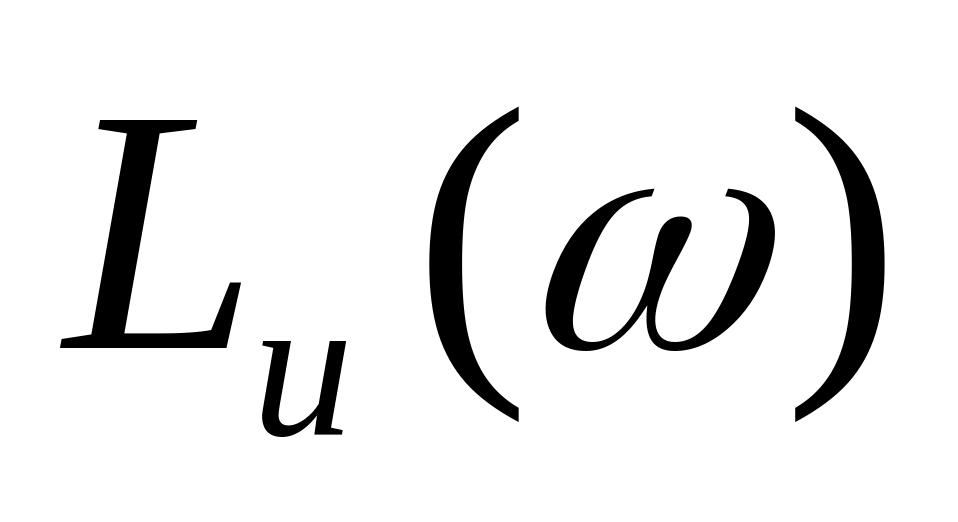 или совмещается с ней. Эта часть
характеристики влияет на плавность
работы системы.
или совмещается с ней. Эта часть
характеристики влияет на плавность
работы системы.
Итак, на первом
этапе построения
частоты, на которых сопрягается
среднечастотная асимптота с сопрягающими
асимптотами, находятся из условий
![]() .
На втором этапе уточняются значения
сопрягающих частот с учетом избытков
фазы. На третьем этапе корректируются
все сопрягающие частоты
по условию их близости к сопрягающей
частоте исходной системы, т. е.
.
На втором этапе уточняются значения
сопрягающих частот с учетом избытков
фазы. На третьем этапе корректируются
все сопрягающие частоты
по условию их близости к сопрягающей
частоте исходной системы, т. е.
![]() ,
если эти частоты незначимо отличаются
друг от друга.
,
если эти частоты незначимо отличаются
друг от друга.
