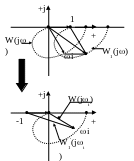
1. Система, устойчивая в разомкнутом состоянии

Пусть введем вспомогательную функцию заменим pj, тогда

Согласно принципа аргумента изменение аргумента D(j) и D_з(j) при 0<< равно Тогда то есть годограф W₁(j) не должен охватывать начало координат.

Для упрощения анализа и расчетов сместим начало радиуса-вектора из начала координат в точку (-1, j0), а вместо вспомогательной функции W₁(j) используем АФХ разомкнутой системы W(j).

Формулировка критерия №1

Если разомкнутая цепь системы устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой цепи не охватывала точку (-1, j0).

35. Методика построения логарифмической частотной характеристики сау: параллельное соединение звеньев.

Передаточные функции последовательно-параллельной цепи преобразуем следующим образом:

Тогда ЛЧХ системы определяются по уравнениям:

где

L_1() и могут быть построены по номограмме замыкания, используя ЛЧХ динамических звеньев:

Структурную схему сколь угодно сложного вида можно упростить и построить логарифмические частотные характеристики.

36. Анализ качества сау в динамике.

Оценка качества САУ в динамике проводится по показателям качества процесса управления, которые делятся на:

- прямые оценки переходного процесса, вызываемого наиболее характерным единичным ступенчатым воздействием;

- косвенные приближённые оценки качества: частотные, интегральные, корневые.

К частотным оценкам относятся: запасы устойчивости по модулю L и по фазе , оценки переходных процессов по ВЧХ и АФХ, показатель колебательности М.

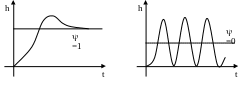Интегральные оценки (линейная, квадратичная, улучшенная квадратичная) одним числом характеризуют и отклонение регулируемой функции, и продолжительность переходного процесса.

Корневые оценки характеризуют степень устойчивости и колебательность (диаграмма И.А. Вышнеградского, корневые годографы).

Прямые показатели качества сау

Рассматривается САУ с единичной ООС.

1. Показатели точности работы САУ.

Установившаяся ошибка выходной функции, определяющая статическую точность системы:

1.2. Динамическая ошибка системы

2. Показатели быстродействия САУ.

2.1. Время регулирования (время затухания переходного процесса) t_p – время от начала процесса отработки входного воздействия до момента, после которого регулируемая функция отличается от своего установившегося значения на величину менее _рег=5%h_уст.

_рег=(15%)h_уст – ошибка регулирования – заданное значение, определяющее точность регулирования.

2.2. Время нарастания переходной функции до максимального значения t_м.

3. Показатели плавности протекания переходного процесса (показатели демпфирования системы).

3.1. Перерегулирование

3.2. Число перерегулирований N за время регулирования, определяемое как число максимумов, для которых h_max-h_уст > _рег.

3.3. Частота колебаний переходного процесса где T_к – период затухания колебаний.

3.4. Скорость затухания переходного процесса оценивается по значению показателя огибающей экспоненты

или

3.5. Степень колебательности переходного процесса

3.6. Число колебаний за время регулирования t_p

χ ,

где T_к – период колебаний, равный расстоянию вдоль оси t между двумя смежными максимумами.

Переходная характеристика по каналу возмущения у астатических систем имеет вид

Здесь h_f()=0. Вместо перерегулирования здесь используется максимальное отклонение выходной функции h_fmax1. Если f(t)=a1(t), то оценка плавности h_max1/a. Ошибка регулирования =(0,010,05)h_p, где h_p – установившееся значение выходной функции по каналу возмущения объекта управления, либо принимается такой же, как и по каналу управления.

Время регулирования, скорость затухания и степень колебательности переходного процесса определяются аналогично показателям h(t).