Уравнения шредингера (общие свойства)

-----------------------------------------------------------------------

1. Стационарное уравнение Шредингера имеет вид . Это уравнение описывает …

	линейный гармонический осциллятор
	движение свободной частицы
	электрон в трехмерном потенциальном ящике
	электрон в водородоподобном атоме

-----------------------------------------------------------------------

Решение: Стационарное уравнение Шредингера в общем случае имеет вид . Здесь  – потенциальная энергия микрочастицы. В данной задаче  соответствует гармоническому осциллятору, то есть движению частицы под действием квазиупругой силы. Следовательно, данное уравнение описывает движение частицы под действием квазиупругой силы, то есть линейный гармонический осциллятор.

-----------------------------------------------------------------------

2. Стационарное уравнение Шредингера описывает линейный гармонический осциллятор, если потенциальная энергия имеет вид …

-----------------------------------------------------------------------

Решение: Стационарное уравнение Шредингера в одномерном случае имеет вид  Здесь  – потенциальная энергия. Выражение  представляет собой потенциальную энергию линейного гармонического осциллятора. В этом случае уравнение Шредингера описывает линейный гармонический осциллятор.

-----------------------------------------------------------------------

3. Верным для уравнения Шредингера является утверждение, что оно …

	является нестационарным
	соответствует одномерному случаю
	является стационарным
	описывает состояние микрочастицы в одномерном бесконечно глубоком прямоугольном потенциальном ящике

-----------------------------------------------------------------------

Решение: Уравнение  называют нестационарным (временным) уравнением Шредингера, так как функция  является функцией не только пространственных координат, но и времени, и оно содержит производную от функции  по времени.

-----------------------------------------------------------------------

4. Верным для уравнения Шредингера , где = const является утверждение:

	Уравнение характеризует движение микрочастицы в области пространства, где потенциальная энергия – постоянная величина.
	Уравнение соответствует трехмерному случаю.
	Уравнение является нестационарным.
	Уравнение описывает линейный гармонический осциллятор.

-----------------------------------------------------------------------

Решение: Уравнение стационарно, так как волновая функция  не зависит от времени (отсутствует производная по времени). Стационарное уравнение Шредингера в общем случае имеет вид: . Здесь  потенциальная энергия микрочастицы. По условию  const. Для гармонического осциллятора . Поэтому из приведенных утверждений верным является следующее: «Уравнение характеризует движение микрочастицы в области пространства, где потенциальная энергия – постоянная величина».

-----------------------------------------------------------------------

5. Стационарное уравнение Шредингера в общем случае имеет вид . Здесь  потенциальная энергия микрочастицы. Трехмерное движение свободной частицы описывает уравнение  …

-----------------------------------------------------------------------

Решение: Свободной называется частица, не подверженная действию силовых полей. Это означает, что . Поэтому трехмерное движение свободной частицы описывает уравнение .

-----------------------------------------------------------------------

6. Стационарное уравнение Шредингера в общем случае имеет вид . Здесь 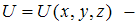 потенциальная энергия микрочастицы. Электрону в одномерном потенциальном ящике с бесконечно высокими стенками соответствует уравнение …

-----------------------------------------------------------------------

Решение: Для одномерного случая . Кроме того, внутри потенциального ящика U = 0, а вне ящика частица находиться не может, так как его стенки бесконечно высоки. Поэтому уравнение Шредингера для частицы в одномерном ящике с бесконечно высокими стенками имеет вид .

-----------------------------------------------------------------------