Отношение длин волн де Бройля для протона и α-частицы, имеющих одинаковую кинетическую энергию, равно …
|
2 |
|
1/2 |
|
4 |
|
1/4 |
-----------------------------------------------------------------------
Решение:
Длина
волны де Бройля определяется по формуле
где
p
– импульс частицы. Импульс частицы
можно выразить через ее кинетическую
энергию:
Тогда
отношение длин волн де Бройля для
протона и α-частицы, имеющих одинаковую
кинетическую энергию,
При
этом учтено, что α-частица, состоящая
из двух протонов и двух нейтронов, имеет
массу
-----------------------------------------------------------------------
Отношение длин волн де Бройля для молекул водорода и кислорода, соответствующих их наиболее вероятным скоростям при одной и той же температуре, равно …
|
4 |
|
|
|
2 |
|
|
-----------------------------------------------------------------------
Решение:
Длина
волны де Бройля определяется
формулой
где
–
постоянная Планка,
и
–
масса и скорость частицы. Наиболее
вероятная скорость молекулы
Здесь
k
– постоянная Больцмана, R
– универсальная газовая постоянная,
–
молярная масса газа. Тогда
-----------------------------------------------------------------------
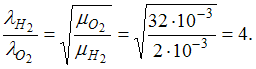
Время жизни атома в возбужденном состоянии 10 нс. Учитывая, что постоянная Планка
,
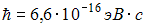ширина энергетического уровня (в эВ)
составляет не менее …
|
|
|
|
|
|
|
|
-----------------------------------------------------------------------
Решение:
Соотношение
неопределенностей для энергии и времени
имеет вид
,
где
неопределенность
в задании энергии (ширина энергетического
уровня),
время
жизни частицы в данном состоянии. Тогда
-----------------------------------------------------------------------
Если молекула водорода, позитрон, протон и -частица имеют одинаковую длину волны де Бройля, то наибольшей скоростью обладает …
|
позитрон |
|
молекула водорода |
|
протон |
|
-частица |
-----------------------------------------------------------------------
Решение:
Длина
волны де Бройля определяется формулой
,
где
–
постоянная Планка,
и
–
масса и скорость частицы. Отсюда скорость
частицы равна
.
По условию задания
,
следовательно,
.
Тогда наибольшей скоростью обладает
частица с наименьшей массой. Известно,
что
.
Следовательно, наибольшей скоростью
обладает позитрон.
-----------------------------------------------------------------------
Положение пылинки массой можно установить с неопределенностью . Учитывая, что постоянная Планка , неопределенность скорости (в м/с) будет не менее …
|
|
|
|
|
|
|
|
-----------------------------------------------------------------------
Решение:
Из
соотношения неопределенностей
Гейзенберга для координаты и
соответствующей компоненты импульса
следует,
что
,
где
–
неопределенность координаты,
–
неопределенность x-компоненты импульса,
–
неопределенность x-компоненты скорости,
–
масса частицы;
–
постоянная Планка, деленная на
.
Неопределенность x-компоненты скорости
пылинки можно найти из соотношения
-----------------------------------------------------------------------