1. Определители второго и третьего порядка и их вычисление. Определение определителя любого порядка. Алгебраические дополнения. Перечислить свойства определителя.

Определитель (детерминант) – число, которое ставится в соответствие квадратной таблице чисел по определенным правилам.

Определитель второго порядка: = =

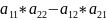
При транспонировании определитель не меняется.

Определитель = 0, когда:

или =0

Определитель 3-го порядка -

или

(минор 1 элемента) (минор 2 элемента) (минор 3 элемента)

Если минор домножить на «-», то он становится алгебраическим дополнением.

A_ij=M_ij*(-1)^i+j

Определитель n-ого порядка:

Свойства:

1. При транспонировании определитель не меняется.

2. При перестановке любых 2 строк(столбцов) определитель меняет знак.

3. Если в определителе 2 строки (столбца) одинаковы, то определитель = 0.

4. Если какая либо строка или столбец состоит только из 0, то определитель = 0.

5. Если в определителе 2 строки или 2 столбца пропорциональны, то определитель = 0.

6. Число, умноженное на определитель = определителю у которого одна строка или столбец умножена на это число.

7. Пусть 2 определителя отличаются только 2 строками, тогда сумма определителя = определителю, у которого одинаковые строки остаются, а не одинаковые складываются. Пример:

8. Если какая то строка является линейной комбинацией остальных строк, то определитель = 0.

9. Если в какой-либо строке добавить линейную комбинацию каких-нибудь других строк, то определитель не меняется.

10. Определитель = сумме произведений элементов какой-либо одной строки на их алгебраическое дополнение.

11. Сумма произведений элементов какой-либо строки (или какого-либо столбца) определителя на соответствующие алгебраические дополнения элементов любой другой строки (любого другого столбца) равна нулю.

12. Определитель = 0,  какая-либо строка является линейной комбинацией другой строки.

Будем говорить, что некоторая строка (а₁, a₂, ..., а_n) является линейной комбинацией строк (b₁, b₂, ...,b_n), (c₁ c₂, ..., c_n), .... (d₁ d₂, .... d_n) с коэффициентами λ, μ, ...,ν, если а_j= λb_j + μc_j + ... + νd_j для всех j— 1, 2, .... n.

2. Определение вектора. Равенство векторов. Сумма векторов и ее свойства. Произведения векторов и числа и его свойства.

Геометрическим вектором (или просто вектором) называется направленный отрезок.

Отрезок называется направленным, если указано, какая из ограничивающих его точек считается началом, какая – концом.

Два вектора называются равными, если они коллинеарные, имеют одинаковую длину и одинаковое направление. Все нулевые векторы считаются равными.

Вектор называется нулевым, если начало и конец его совпадают.

Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.

Из определения равенства векторов непосредственно вытекает следующее утверждение: каковы бы ни были вектор а и точка Р, существует, и притом единственный, вектор PQ с началом в точке Р, равный вектору а.

Суммой a + b двух векторов a и b называется вектор, идущий из начала вектора a в конец вектора b

при условии, что вектор b приложен к концу вектора a.

Правило сложения двух векторов, содержащееся в этом определении, обычно называют правилом треугольника.

Свойства:

1. а + b = b + а (переместительное свойство);

2. (а + b) + с = а + (b + с) (сочетательное свойство);

3. Существует нулевой вектор 0 такой, что a + 0 = a для любого вектора a (особая роль нулевого вектора);

4. Для каждого вектора a существует противоположный ему вектор a’ такой, что a + a’ = 0.

Произведением αа (или аα) вектора a на вещественное число α называется вектор Ь, коллинеарный вектору а, имеющий длину, равную |а|*|α|, и имеющий направление, совпадающее с направлением вектора а в случае а > 0 и противоположное направлению вектора а в случае а < 0.

Свойства:

1. α(a + b)= αa + αb (распределительное свойство числового сомножителя относительно суммы векторов);

2. (α + β)а = αа + βа (распределительное свойство векторного сомножителя относительно суммы чисел);

3. α(βа) = (αβ)a (сочетательное свойство числовых сомножителей).

Эти свойства имеют фундаментальное значение, ибо они позволяют производить выкладки в векторной алгебре по тем правилам, по которым производятся аналогичные выкладки в обычной алгебре.