- •1. Механическое движение. Система отсчета, системы координат. Перемещение, траектория, путь. Скорость. Ускорение.
- •2. Прямолинейное и криволинейное движение. Кинематика вращательного движения. Кинематические уравнения движения.
- •3. Классическая динамика частиц. Понятие состояния частицы в классической механике. Основная задача динамики.
- •4. Первый закон Ньютона. Понятие инерциальной системы отсчета.
- •5. Масса и импульс тела. Второй закон Ньютона. Уравнение движения.
- •6. Третий закон Ньютона. Понятие о механической системе. Импульс тела и импульс силы.
- •7. Закон сохранения импульса тела и системы тел.
- •31. Специальная теория относительности. Преобразование Лоренца. Интервал. Границы применимости ньютоновской механики.
- •33. Релятивистский импульс. Релятивистское выражение для энергии. Релятивистский импульс
- •34. Преобразование импульса и энергии. Взаимосвязь массы и энергии покоя. Частицы с нулевой массой.
- •Нулевая масса
- •35. Гравитация. Закон всемирного тяготения. Гравитационное поле.
- •36. Космические скорости.
- •37. Принцип эквивалентности. Понятие об общей теории относительности.
- •38. Колебательное движение. Гармонические колебания. Векторная диаграмма.
- •Кинематика гармонических колебаний
- •Динамика гармонических колебаний
- •39. Маятники (математический, физический, оборотный).
- •41. Затухающие колебания. Автоколебания. Вынужденные колебания. Параметрический резонанс.
- •42. Свободные затухающие колебания.
- •43. Распространение волн в упругой среде. Уравнение плоской и сферической волн. Скорость упругих волн в твердой средой среде. Эффект Доплера для звуковых волн.
- •44. Энергия упругой волны. Поток энергии в упругой волне.
- •45. Стоячие волны. Колебания струны. Звук. Скорость звука в газах.
- •46. Масса и размер молекул. Состояние термодинамической системы. Температура.
- •[Править]Классификация
- •47. Уравнение состояния идеального газа.
- •48. Внутренняя энергия термодинамической системы. Внутренняя энергия и температура термодинамической системы
- •49. Процесс. Первое начало термодинамики.
- •50. Работа, совершаемая телом при изменении объема.
- •51. Внутренняя энергия и теплоемкость идеального газа.
- •Внутренняя энергия и теплоемкость идеального газа.
- •52. Уравнение Адиабаты идеального газа.
- •Уравнение Пуассона. Работа газов.
- •53. Политропические процессы. Работа, совершаемая газом при различных процессов.
- •Показатель политропы
- •55. Барометрическая формула.
- •56. Характер теплового движения молекул. Число ударов молекул о стену. Определение Перреном постоянной Авогадро.
- •57. Средняя энергия молекул. Средняя кинетическая энергия теплового движения молекул.
- •Распределение молекул по скоростям.
- •58. Распределение Максвелла. Экспериментальная проверка закона распределения Максвелла.
- •59. Распределение Больцмана.
- •60. Энтропия. Вычисление Энтропия.
38. Колебательное движение. Гармонические колебания. Векторная диаграмма.
Колебательное движение – это периодическое движение, которое совершается поочерёдно в двух противоположных направлениях.
Кинематика гармонических колебаний
Уравнение
гармонических колебаний:
![]() ,
,
где
![]() -
смещение
колеблющейся точки от положения
равновесия; t
- время;
-
смещение
колеблющейся точки от положения
равновесия; t
- время;
![]() ,
,
![]() и
и
![]() -
соответственно амплитуда, угловая
частота и начальная фаза колебаний;
-
соответственно амплитуда, угловая
частота и начальная фаза колебаний;
![]() -
фаза колебаний в момент времени t.
-
фаза колебаний в момент времени t.
Скорость
точки при гармонических колебаниях:
![]() ,
,
Максимальная
скорость точки при гармонических
колебаниях:
![]() ,
,
Ускорение
точки при гармонических колебаниях:
![]() ,
,
Максимальное
ускорение точки при гармонических
колебаниях:
![]() ,
,
Кинетическая
энергия точки при гармонических
колебаниях:
![]() ,
,
Максимальная
кинетическая энергия точки при
гармонических колебаниях:
![]()
Потенциальная
энергия точки при гармонических
колебаниях:
![]()
Максимальная
потенциальная энергия точки при
гармонических колебаниях:
![]() ,
,
Закон
сохранения энергии при механических
колебаниях:
![]() ,
,
Динамика гармонических колебаний
Результирующая сила, действующая на точку при гармонических колебаниях:
![]() ,
где
,
где
![]() -
коэффициент жёсткости.
-
коэффициент жёсткости.
Максимальная сила, действующая на точку при гармонических колебаниях:
![]() .
.
Период
колебаний математического маятника:
![]() .
.
Период
пружинного математического маятника:
![]() .
.
Связь
периода гармонических колебаний с
частотой и циклической частотой
колебаний:
![]() .
.
39. Маятники (математический, физический, оборотный).
Ма́ятник — система, подвешенная в поле тяжести и совершающая механические колебания. Колебания совершаются под действием силы тяжести, силы упругости и силы трения. Во многих случаях трением можно пренебречь, а от сил упругости (либо сил тяжести) абстрагироваться, заменив их связями.
Во время колебаний маятника происходят постоянные превращения энергии из одного вида в другой. Кинетическая энергия маятника превращается в потенциальную энергию (гравитационную, упругую) и обратно. Кроме того, постепенно происходит диссипация кинетической энергии в тепловую за счёт сил трения.
Одним из простейших маятников является шарик, подвешенный на нити. Идеализацией этого случая является математический маятник — механическая система, состоящая из материальной точки, подвешенной на невесомой нерастяжимой нити или на невесомом стержне в поле тяжести.
Если размерами массивного тела пренебречь нельзя, но всё еще можно не учитывать упругих колебаний тела, то можно прийти к понятию физического маятника. Физический маятник — твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной горизонтальной оси, не проходящей через центр масс этого тела.
Система из нескольких шариков, подвешенных на нитях в одной плоскости, колеблющихся в этой плоскости и соударяющихся друг с другом, называетсямаятником Ньютона. Здесь уже приходится учитывать упругие процессы.
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомойнерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины Lнеподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
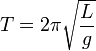
и не зависит[2] от амплитуды колебаний и массы маятника.
Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.
Уравнение колебаний маятника
Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида
![]()
где ![]() ―
положительная константа, определяемая
исключительно из параметров маятника.
Неизвестная функция
―
положительная константа, определяемая
исключительно из параметров маятника.
Неизвестная функция ![]() ―
это угол отклонения маятника в момент
―
это угол отклонения маятника в момент ![]() от
нижнего положения равновесия, выраженный
в радианах;
от
нижнего положения равновесия, выраженный
в радианах; ![]() ,
где
,
где ![]() ―
длина подвеса,
―
длина подвеса, ![]() ― ускорение
свободного падения.
Уравнение малых колебаний маятника
около нижнего положения равновесия
(т. н. гармоническое уравнение) имеет
вид:
― ускорение
свободного падения.
Уравнение малых колебаний маятника
около нижнего положения равновесия
(т. н. гармоническое уравнение) имеет
вид:
![]() .
.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:
![]() .
.
Полагая ![]() ,
предыдущее уравнение можно переписать
в виде:
,
предыдущее уравнение можно переписать
в виде:
![]() .
.
Последнее
уравнение аналогично уравнению
колебаний математического
маятника длиной ![]() .
Величина
называется приведённой
длиной физического
маятника.
.
Величина
называется приведённой
длиной физического
маятника.
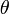 —
угол отклонения
маятника от равновесия;
—
угол отклонения
маятника от равновесия;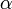 —
начальный угол
отклонения маятника;
—
начальный угол
отклонения маятника;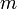 —
масса маятника;
—
масса маятника;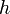 —
расстояние от
точки подвеса до центра тяжести маятника;
—
расстояние от
точки подвеса до центра тяжести маятника; —
радиус инерции
относительно оси, проходящей через
центр тяжести.
—
радиус инерции
относительно оси, проходящей через
центр тяжести.— ускорение свободного падения.
Момент инерции относительно оси, проходящей через точку подвеса:
![]() .
.
ОБОРОТНЫЙ МАЯТНИК -
прибор для эксперим. определения ускорения
свободного падения g.
Представляет собой физ. маятникв
виде, напр., массивной пластины (рис.) с
двумя трёхгранными ножами, из к-рых один
неподвижен, а другой может перемещаться
вдоль прорези на пластине. Острые рёбра
ножей О1 и О2,
помещаемые попеременно на неподвижную
опору, служат осями качаний О. м. Подвижный
нож перемещают вверх или вниз до тех
пор, пока периоды колебаний О. х. вокруг
каждой из осей не совпадут. Расстояние
О1О2 = l между
осями измеряют с помощью нанесённой на
пластину шкалы с нониусом. Тогда по
свойствам физ. маятникаО2 будет
для О1 центром
качаний, и наоборот, а период малых
колебаний О. м. будет при этом равен![]() Зная
значения Т и l из
опыта, можно по данной ф-ле вычислить g.
О. м. позволяет определить величину g со
значительно более высокой степенью
точности, чем матем. маятник.
Зная
значения Т и l из
опыта, можно по данной ф-ле вычислить g.
О. м. позволяет определить величину g со
значительно более высокой степенью
точности, чем матем. маятник.
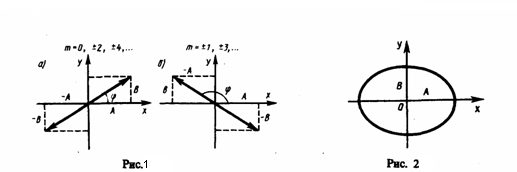
40. Сложение взаимно перпендикулярных колебаний.
|
|
|