
- •1. Механическое движение. Система отсчета, системы координат. Перемещение, траектория, путь. Скорость. Ускорение.
- •2. Прямолинейное и криволинейное движение. Кинематика вращательного движения. Кинематические уравнения движения.
- •3. Классическая динамика частиц. Понятие состояния частицы в классической механике. Основная задача динамики.
- •4. Первый закон Ньютона. Понятие инерциальной системы отсчета.
- •5. Масса и импульс тела. Второй закон Ньютона. Уравнение движения.
- •6. Третий закон Ньютона. Понятие о механической системе. Импульс тела и импульс силы.
- •7. Закон сохранения импульса тела и системы тел.
- •31. Специальная теория относительности. Преобразование Лоренца. Интервал. Границы применимости ньютоновской механики.
- •33. Релятивистский импульс. Релятивистское выражение для энергии. Релятивистский импульс
- •34. Преобразование импульса и энергии. Взаимосвязь массы и энергии покоя. Частицы с нулевой массой.
- •Нулевая масса
- •35. Гравитация. Закон всемирного тяготения. Гравитационное поле.
- •36. Космические скорости.
- •37. Принцип эквивалентности. Понятие об общей теории относительности.
- •38. Колебательное движение. Гармонические колебания. Векторная диаграмма.
- •Кинематика гармонических колебаний
- •Динамика гармонических колебаний
- •39. Маятники (математический, физический, оборотный).
- •41. Затухающие колебания. Автоколебания. Вынужденные колебания. Параметрический резонанс.
- •42. Свободные затухающие колебания.
- •43. Распространение волн в упругой среде. Уравнение плоской и сферической волн. Скорость упругих волн в твердой средой среде. Эффект Доплера для звуковых волн.
- •44. Энергия упругой волны. Поток энергии в упругой волне.
- •45. Стоячие волны. Колебания струны. Звук. Скорость звука в газах.
- •46. Масса и размер молекул. Состояние термодинамической системы. Температура.
- •[Править]Классификация
- •47. Уравнение состояния идеального газа.
- •48. Внутренняя энергия термодинамической системы. Внутренняя энергия и температура термодинамической системы
- •49. Процесс. Первое начало термодинамики.
- •50. Работа, совершаемая телом при изменении объема.
- •51. Внутренняя энергия и теплоемкость идеального газа.
- •Внутренняя энергия и теплоемкость идеального газа.
- •52. Уравнение Адиабаты идеального газа.
- •Уравнение Пуассона. Работа газов.
- •53. Политропические процессы. Работа, совершаемая газом при различных процессов.
- •Показатель политропы
- •55. Барометрическая формула.
- •56. Характер теплового движения молекул. Число ударов молекул о стену. Определение Перреном постоянной Авогадро.
- •57. Средняя энергия молекул. Средняя кинетическая энергия теплового движения молекул.
- •Распределение молекул по скоростям.
- •58. Распределение Максвелла. Экспериментальная проверка закона распределения Максвелла.
- •59. Распределение Больцмана.
- •60. Энтропия. Вычисление Энтропия.
33. Релятивистский импульс. Релятивистское выражение для энергии. Релятивистский импульс
Выражение, обеспечивающее инвариантность закона сохранения импульса, может быть получено, если вместо времени t подставить собственное время τ.
Тогда 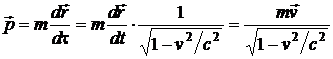 .
.
Релятивистское выражение для энергии
В релятивистской механике справедливым остается выражение
![]() .
.
Это
означает, что 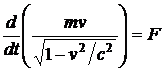 .
Откуда видно, что сила не является
инвариантной величиной. Кроме того,
сила F и
ускорение a не
коллинеарны.
.
Откуда видно, что сила не является
инвариантной величиной. Кроме того,
сила F и
ускорение a не
коллинеарны.
Легко получить выражение для кинетической энергии. Поскольку
dEk = dA и dEk = v·p·dt, dA = F·ds
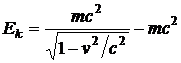 .
.
Отсюда следует, что E0 = mc2 является энергией покоя. Энергия и импульс в релятивистской механике не сохраняются. Инвариантом является выражение:
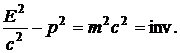
Взаимосвязь массы и энергии. Границы применимости механики Ньютона.
34. Преобразование импульса и энергии. Взаимосвязь массы и энергии покоя. Частицы с нулевой массой.
Преобразования импульса и энергии.
Если в соотношении (8.3) учесть выражения для релятивистской энергии (8.10) и энергии покоя (8.12), то получим
![]()
![]()
![]() ,
(8.14)
,
(8.14)
которая выражает связь между энергией и импульсом в релятивистской механике. Заметим, что величина
![]()
![]() ,
(8.15)
,
(8.15)
которая
является квадратом энергии покоя
частицы, инвариантна относительно
преобразований Лоренца, хотя релятивистский
импульс и энергия меняются при
переходе ![]()
![]() .
Эти формулы преобразования можно
получить, пользуясь формулами
преобразования релятивистских скоростей.
Например,
.
Эти формулы преобразования можно
получить, пользуясь формулами
преобразования релятивистских скоростей.
Например,
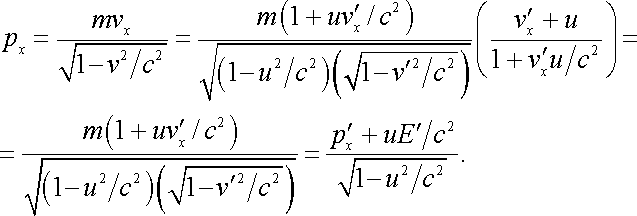
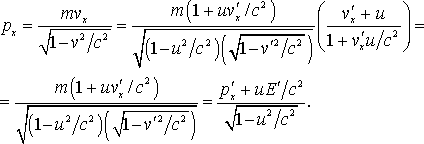
Подобным же образом получим остальные преобразования:
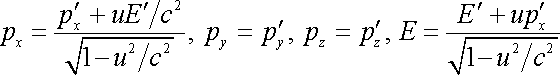
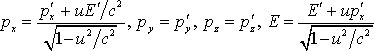 .
(8.16)
.
(8.16)
Заметим, что величины
![]()
![]() (8.17)
(8.17)
преобразуются по одним и тем же формулам, что и координаты события x, y, z, t, т.е. составляют лоренцева группу.
Нетрудно проверить, пользуясь формулами преобразования энергии и импульса (8.16), что
![]()
![]() ,
(8.15´)
,
(8.15´)
которое
с точностью до постоянного
множителя ![]()
![]() совпадает
с (8.15).
совпадает
с (8.15).
Приведем еще два полезных соотношения. Из формул релятивистской энергии и импульса следует, что
![]()
![]() (8.18)
(8.18)
а с учетом (8.11) из (8.15) получаем
![]()
![]() .
(8.19)
.
(8.19)
Последнее
есть связь
между кинетической энергией и импульсом в
релятивистской механике. В случае
медленных движений частицы, когда ![]()
![]() ,
(8.19) дает классическую связь кинетической
энергии и импульса:
,
(8.19) дает классическую связь кинетической
энергии и импульса:
![]()
![]() ,
(8.20)
,
(8.20)
а
в противоположном пределе
- ![]()
![]() (ультрарелятивистское
движение)-
(ультрарелятивистское
движение)-
![]()
![]() .
(8.21)
.
(8.21)
Взаимосвязь массы и энергии покоя |
|
|
|
Масса и энергия покоя связаны уравнением:
из которого вытекает, что всякое изменение массы Δm сопровождается изменением энергии покоя ΔE0 : ΔE0 = Δm c2 Это утверждение носит название закона взаимосвязи массы и энергии покоя, оно стало символом современной физики. Взаимосвязь между массой и энергией оценивалась А. Эйнштейном как самый значительный вывод специальной теории относительности. По его выражению, масса должна рассматриваться как «сосредоточение колоссального количества энергии». При этом масса в теории относительности не является более сохраняющейся величиной, а зависит от выбора системы отсчета и характера взаимодействия между частицами. Определим энергию, содержащуюся в 1 г любого вещества, и сравним ее с химической энергией, равной 2,9·104 Дж, получаемой при сгорании 1 г угля. Согласно уравнению Эйнштейна E = mc2, имеем
Таким образом, собственная энергия в 3,1·108 раз превышает химическую энергию. Из этого примера видно, что если высвобождается лишь одна тысячная доля собственной энергии, то и это количество в миллионы раз больше того, что могут дать обычные источники энергии. Суммарная масса взаимодействующих частиц не сохраняется. Рассмотрим другой пример. Пусть две одинаковые по массе частицы m движутся с одинаковыми по модулю скоростями навстречу друг другу и абсолютно не упруго столкнутся.
До
соударения полная энергия каждой
частицы Е равна:
отсюда М равно:
Таким образом, сумма масс исходных частиц 2m меньше массы образовавшейся частицы М. В этом примере, кинетическая энергия частиц превратилась в эквивалентное количество энергии покоя, а это привело к возрастанию массы:
(это при отсутствии выделения энергии при соударении частиц). Выражение «масса покоя» можно употребить как синоним «энергия покоя». Пусть система (ядро) состоит из n частиц с массами m1, m1, ..., mn. Ядро не будет распадаться на отдельные частицы, если они связаны друг с другом. Эту связь можно охарактеризовать энергией связи Eсв. Энергия связи – энергия, которую нужно затратить, чтобы разорвать связь между частицами и разнести их на расстояние, при котором взаимодействием частиц друг с другом можно пренебречь.
где ΔM = m1 + m2 + ... + mn ; ΔM – дефект массы.
Видно,
что Eсв
будет положительна, если При слиянии частиц энергия связи высвобождается (часто в виде электромагнитного излучения). Например, ядро U238 имеет энергию связи Eсв = 2,9·10-10 Дж ≈ 1,8·109 эВ = 1,8 ГэВ. |

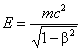 .
Полная энергия образовавшейся частицы
Mc2.
Эта новая частица имеет скорость
υ = 0.
Из закона сохранения энергии:
.
Полная энергия образовавшейся частицы
Mc2.
Эта новая частица имеет скорость
υ = 0.
Из закона сохранения энергии: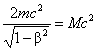 ,
,