30. Понятие вариации и её значение в экономических исследованиях.

Вариация - колеблемость, изменяемость величины признака у единиц совокупности. Отдельные числовые значения признака, встречающиеся в изу­чаемой совокупности, называют вариантами значений. Недостаточность средней величины для полной характеристики совокупности заставляет дополнять средние величины показателями, позволяющими оценить типичность этих средних путем измерения колеблемости (вариации) изучаемого признака.

Наличие вариации обусловлено влиянием большого числа факторов на формирование уровня признака. Эти факторы действуют с неодинаковой силой и в разных направлениях. Для описания меры изменчивости признаков используют показатели вариации.

Задачи статистического изучения вариации:

1) изучение характера и степени вариации признаков у отдельных единиц совокупности;

2) определение роли отдельных факторов или их групп в вариации тех или иных признаков совокупности.

В статистике применяются специальные методы исследования вариации, основанные на использовании системы показателей, с помощью которых изме­ряется вариация.

Исследование вариаций имеет важное значение. Измерение вариаций необходимо при проведении выборочного наблюдения, корреляционном и дисперсионном анализе и т. д.

По степени вариации можно судить об однородности совокупности, об устойчивости отдельных значений признаков и типичности средней. На их основе разрабатываются показатели тесноты связи между признаками, показатели оценки точности выборочного наблюдения.

31. Абсолютные показатели вариации. Общая характеристика, анализ и интерпретация.

Для определения абсолютной меры колеблемости признаков или величины вариации применяются абсолютные средние размеры вариации:

1. Размах вариации – это абсолютная разность между максимальным и минимальным значением признака в изучаемой совокупности. Измеряет только крайние отклонения вариант в ряду

2. Среднее линейное отклонение – определяется из отклонений индивидуальных значений признака от средней величины, без учета знака этих отклонений. Измеряет отклонение каждой варианты (взвешенная)

- простое среднее значение

- взвешенное среднее значение

3. Дисперсия (средний квадрат отклонения) – определяется как среднее из отклонений индивидуальных значений признака от средней величины, возведенной в квадрат

- простая

- взвешенная

4. Среднее квадратическое отклонение – является мерой надежности средней величины, чем оно меньше, тем точнее среднее арифметическое отражает собой всю изучаемую совокупность. Выражается в тех же единицах измерения, что и признак

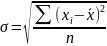– простая

- взвешенная

Среднее квадратическое отклонение по величине всегда больше среднего линейного отклонения. Для нормального закона распределения это отношение

Если это отношение больше, то это свидетельствует о наличие в совокупности резких выделяющихся отклонений. Неоднородно с основной массой элементов, нарушающих развитие основной тенденции или закономерности совокупности

Свойства дисперсии:

1) дисперсия постоянной величины равна 0

2) уменьшение всех значений признака на одну и уже величину А не меняет величину дисперсии

3) уменьшение всех значений признаков в К раз, уменьшает значение дисперсию в К² раз, а среднее квадратическое отклонение в К раз

4) дисперсия любой величины А, в той или иной степени отличающийся от средней арифметической всегда, будет больше дисперсии средней арифметической (свойство минимальности)