27. Виды средних и способы их вычисления.

Средняя арифметическая простая невзвешенная (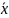 ) – это форма средней используется в тех случаях, когда расчет производится по несгруппированным данным.

, где x_I – значение признака для единицы совокупности, n – количество единиц совокупности

Средняя арифметическая средняя взвешенная ( )– при расчете средних величин отдельные значения осведняемого признака могут повторяться, то есть встречаться по несколько раз. В подобных случаях, расчет средней производится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными.

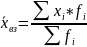
Если данные не сгруппированы применяется простая, если данные сгруппированы применяется взвешенная.

Средняя гармоническая невзвешенная простая – это форма средней, которая используется значительно реже, в основном для сравнения

Средняя гармоническая взвешенная – используется в том случае, когда известен числитель исходного соотношения средней, но не известен его знаменатель.

Средняя геометрическая – применяется для расчета среднего темпа или коэффициента роста статистического показателя

– простая

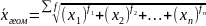- взвешенная

Средняя квадратическая – лежит в основе вычисления ряда сводных расчетных показателей. Наиболее широко этот вид используется при расчете показателей вариации

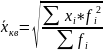- взвешенная

- простая

28. Средняя арифметическая и гармоническая. Правила выбора формы средней.

Средние величины бывают простые и взвешенные. Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на эту численность. Иными словами, «весами» выступают числа единиц совокупности в разных группах, т.е. каждый вариант «взвешивают» по своей частоте. Частоту f называют статистическим весом или весом средней.

Средняя арифметическая простая невзвешенная ( ) – это форма средней используется в тех случаях, когда расчет производится по несгруппированным данным.

, где x_I – значение признака для единицы совокупности, n – количество единиц совокупности

Средняя арифметическая средняя взвешенная ( )– при расчете средних величин отдельные значения осведняемого признака могут повторяться, то есть встречаться по несколько раз. В подобных случаях, расчет средней производится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными.

Если данные не сгруппированы применяется простая, если данные сгруппированы применяется взвешенная.

Средняя гармоническая невзвешенная простая – это форма средней, которая используется значительно реже, в основном для сравнения

Средняя гармоническая взвешенная – используется в том случае, когда известен числитель исходного соотношения средней, но не известен его знаменатель.

29. Структурные средние. Общая характеристика, анализ и интерпретация.

Для характеристики структуры совокупности применяются особые показатели, которые называют структурными средними.

К таким показателям относятся мода (М_О) и медиана (М_Е). В отличие от средней арифметической и средней гармонической мода и медиана совпадают с конкретным числом, имеющимся в вариационном ряду и не всегда совпадают со средней арифметической и средней гармонической.

Модой называется чаще всего встречающийся вариант или то значение признака, которое соответствует максимальной точки теоретической кривой распределения.

Мода в разных рядах распределения:

1. Если ряд дискретный, то мода является значением признака с наибольшей частотой.

2. В интервальном вариационном ряду модой приближенно считают центральный вариант так называемого модального интервала, то есть того интервала, который имеет наибольшую частоту. В пределах этого интервала необходимо найти значение признака, которое является модой. Решение вопроса состоит в том, чтобы в качестве моды выявить середину модального интервала. Такое решение будет правильным лишь в случае полной симметричности распределения либо тогда, когда интервалы, соседние с модальными мало отличаются друг от друга по числу случаев. В противном случае, середина модального интервала не может рассматриваться как мода

Конкретное значение моды для интервального ряда определяется по формуле:

Где: F_mod – нижняя граница модального интервала, I_mod - величина модального интервала, F_mod - частота модального интервала, F_mod-1 - частота, предшествующая частоте модального интервала, F_mod+1 - частота, следующая за частотой модального интервала

Медианой (серединным вариантом) в статистике называют значение варьирующего признака, который находится в середине ряда, расположенного в порядке возрастания или убывания.

Для четного ряда медиана определяется по формуле:

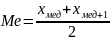
Для интервального вариационного ряда порядок нахождения медианы следующий:

1) располагаем индивидуальные значения признака по ранжиру

2) определяем для данного ранжированного ряда накопленные частоты

3) по данным о накопленных частотах находим медианный интервал

Медианы делят численность ряда пополам, следовательно она там, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая накопленная частота меньше половины численности совокупности

Для определения места медианы в ряду используют следующую формулу

Если предполагать, что внутри медианного интервала нарастание или убывание изучаемого признака происходит по прямой равномерно, то медиана определяется по формуле:

Х_мед -нижняя граница медианного интервала

I_мед - величина медианного интервала

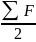- полусумма частот ряда

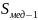- накопленная частота, предшествующая накопленной частоте медианного интервала

F - частота медианного интервала