11. Индексный метод изучение динамики среднего уровня

Средний индекс – это индекс, вычисленный как средняя величина из индивидуальных индексов. ---Средний арифметический индекс объема продукции вычисляется:

, так как .

-Средний гармонический индекс себестоимости можно исчислить так:

.

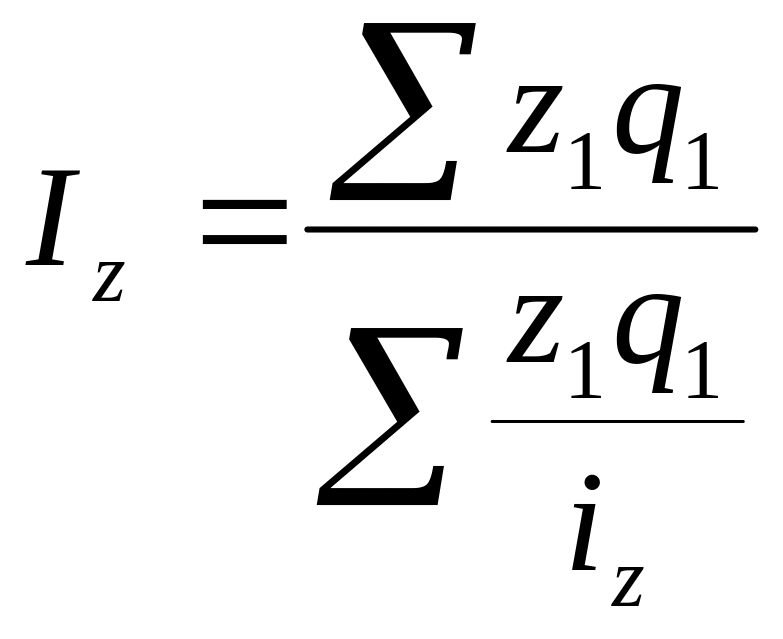индексы постоянного и переменного состава, индексы структурных сдвигов.

Изменение средней величины показателя зависит от двух факторов – изменения значения индексируемого показателя у отдельных единиц и изменения структуры явления. Изменение структуры – это изменение доли отдельных групп единиц совокупности в общей их численности. Задача определения влияния каждого фактора определяется с помощью индексного метода, т.е. путем построения системы взаимосвязанных индексов, в которую включаются три индекса: переменного состава, постоянного состава и структурных сдвигов. Индекс переменного состава – индекс, выражающий соотношение средних уровней изучаемого явления, относящихся в разным периодам времени. Например, индекс переменного состава себестоимости продукции:

.

Индекс постоянного состава – это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Например, индекс фиксированного состава себестоимости продукции:

Индекс структурных сдвигов – индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления:

Система взаимосвязанных индексов при анализе динамики средней себестоимости имеет следующий вид:

11. Сущность, значение и виды выборочного наблюдения.

По охвату единиц совокупности статистическое наблюдение может быть проведено как сплошное и несплошное. Сплошное наблюдение предусмат­ривает обследование всех единиц изучаемой совокупности и свя­зано с большими трудовыми и материальными затратами. Изуче­ние не всех единиц совокупности, а лишь некоторой части, по ко­торой следует судить о свойствах всей совокупности в целом, мож­но осуществить несплошным наблюдением. В статистической прак­тике самым распространенным является выборочное наблюдение Выборочное наблюдение – это такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная часть изучается, а результаты распро­страняются на всю исходную совокупность. Совокупность, из которой производится отбор, называется ге­неральной, и все ее обобщающие показатели – генеральными. Совокупность отобранных единиц именуют выборочной сово­купностью, и все ее обобщающие Понятие репрезентативности отобранной совокупности не следует понимать как ее представительство по всем признакам изучаемой совокупности, а только в отношении тех признаков, которые изучаются или оказывают существенное влияние на формирование сводных обобщающих характеристик.

Виды выборки

-Ошибки регистрации могут иметь случайный (непреднаме­ренный) и систематический (тенденциозный) характер. Случайные ошибки обычно уравновешивают друг друга, поскольку не имеют преимущественного направления в сторону преувеличения или преуменьшения значения изучаемого показателя. Систематические ошибки направлены в одну сторону вследствие преднамеренного нарушения правил отбора (предвзятые цели). Их можно избежать при правильной организации и проведении наблюдения -Ошибки репрезентативности присущи только выборочно­му наблюдению и возникают в силу того, что выборочная сово­купность не полностью воспроизводит генеральную. Они пред­ставляют собой расхождение между значениями показателей, по­лученных по выборке, и значениями показателей этих же вели­чин, которые были бы получены при проведенном с одинаковой степенью точности сплошном наблюдении, т. е. между величи­нами выборных и соответствующих генеральных показателей.

По виду различают индивидуальный, групповой и комби­нированный отбор. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной со­вокупности; при групповом отбо­ре – качественно однородные группы или серии изучаемых единиц; комбинированный отбор предполагает сочетание первого и второго видов.

По методу отбора различают повторную и бесповтор­ную выборки.

-При повторной выборке общая численность единиц генеральной совокупности в процессе выборки остается неизменной. Ту или иную единицу, попавшую в выборку, после регистрации снова возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами при повторном отборе единиц вновь попасть в выборку -При бесповторной выборке единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшем в выборке не участвует; т. е. последующую выборку делают из генеральной совокупности уже без отобранных ранее единиц («отбор по

Основные характеристики параметров гене­ральной и выборочной совокупностей обозначаются символами:

– объем генеральной совокупности (число входящих в нее единиц);

– объем выборки (число обследованных единиц);

– генеральная средняя (среднее значение признака в генеральной совокупности);

– выборочная средняя;

– генеральная доля (доля единиц, обладающих дан­ным значением признака в общем числе единиц генеральной совокупности);

– выборочная доля;

– генеральная дисперсия (дисперсия признака в ге­неральной совокупности);

– выборочная дисперсия того же признака;

– среднее квадратическое отклонение в генеральной совокупности;

– среднее квадратическое отклонение в выборке.

17.статистическое изучние взаимосвязи социально-экономических явлений. Корреляционный анализ. Показатели тесноты связи.

18. дисперсия, ее виды. Правило сложение дисперсию

Дисперсия – средний квадрат отклонений значений признака от их средней величины.

Невзвешенная формула:

Взвешенная формула:

1⁰ Дисперсия постоянной величины равна 0

2⁰ Уменьшение всех значений признака на одну и ту же величину А не изменяет величину дисперсии

3⁰ Уменьшение всех значений признака в В раз уменьшает дисперсию в В² раз, а среднее квадратическое отклонение в В раз

Таким образом все значения признака можно разделить на какую-то постоянную величину, затем определить среднее квабратическое отклонение и умножить его на эту постоянную величину

4⁰ Средний квадрат отклонений от любой величины А в той или иной степени отличающейся от средней арифметической всегда будет больше среднего квадрата отклонений, исчисленного от средней арифметической

При этом средний квадрат отклонений будет больше на определенную величину (на квадрат разности средней и условно взятой величины)

5⁰ Дисперсия имеет свойство минимальности; если А=0, то дисперсия вычисляется по формуле:

Правило трех

1) В пределах располагается 68,3% количества наблюдений

2) В пределах находится 95,4% количества наблюдений

3) В пределах находится 99,7% количества наблюдений

Отклонения считается максимально возможными

Правило сложения дисперсии.

- общая дисперсия;

- средняя из внутригрупповых дисперсий;

- межгрупповая дисперсия.

Общая дисперсия измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию.

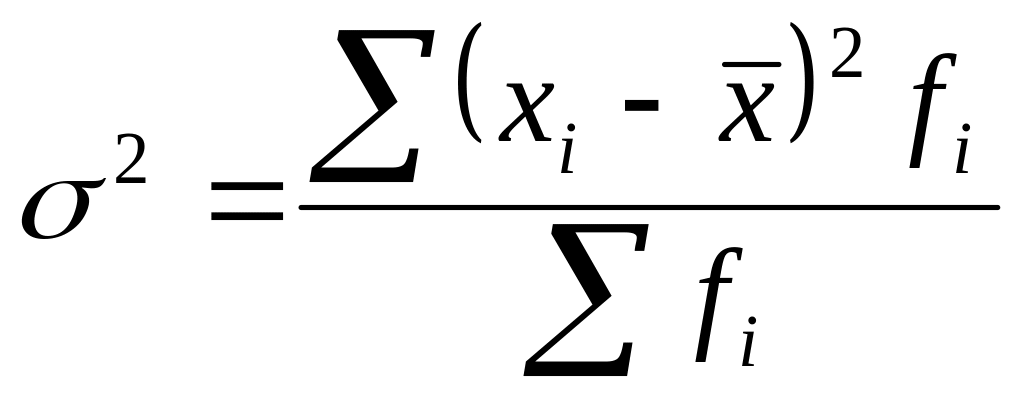
Межгрупповая дисперсия отражает ту часть вариации результативного признака, которая обусловлена воздействием факторного признака. Это воздействие проявляется в отклонении групповых средних от общей средней:

где - среднее значение результативного признака по i-ой группе;

- общая средняя по совокупности в целом;

- объем (численность) i-ой группы.

Если факторный признак, по которому производится группировка, не оказывает никакого влияния на результативный признак, то групповые средние будут равны между собой и совпадут с общей средней. В этом случае межгрупповая средняя будет равна нулю. Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и независящую от признака фактора, положенного в основание группировки.

Средняя из внутригрупповых дисперсий отражает ту часть вариации результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка:

где - дисперсия результативного признака в i-ой группе;

- объем (численность) i-ой группы;

Эмпирический коэффициент детерминации представляет собой долю межгрупповой дисперсии в общей дисперсии.

Теснота связи между факторным и результативным признаком оценивается на основе эмпирического корреляционного отношения:

Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.