
- •Комплексные числа. Алгебраическая и тригонометрическая формы.
- •Арифметические действия с Арифметические действия с комплексными числами в алгебраической форме.
- •Арифметические действия с комплексными числами в тригонометрической форме.
- •Функция комплексного переменного.
- •Предел и непрерывность функции комплексного переменного
- •Производная функции комплексного переменного. Аналитичность функции. Условие Коши-Римана
- •Понятие конфортного отображения
- •Элементарные функции комплексного переменного: ez, sin z, cos z
- •Степенная функция
- •Гиперболические функции
- •Интеграл фкп, его свойства и вычисление.
- •Интеграл
- •Теорема Коши
- •Теорема Коши для многосвязной функции.
- •Интеграл от аналитической функции. Первообразная.
- •Интегральная теорема Коши. Производная n-го порядка от аналитической функции.
- •Ряд Тейлора и ряд Лорана.
- •Регулярные и особые точки функции. Классификация особых точек. Связь между нулем и полюсом функции.
- •Вычет функции. Основная теорема о вычетах
- •Вычет функции относительно простого полюса и полюса порядка m.
- •Вычисление несобственных интегралов с помощью вычетов.
- •Вычисление определенных интегралов с помощью вычетов.
- •Интегральное преобразование Лапласа
- •Оригиналы и изображения.
- •Свойства преобразования Лапласа, теоремы линейности, теорема дифференцируемости оригинала.
- •Теоремы затухания, дифференцирования по параметру, подобия и затухания.
- •45. Метод функции Ляпунова. Теорема Четаева.
- •46. Основные уравнения математической физики: волновое, теплопроводности, Пуассона, Лапласа.
- •Комплексные числа. Алгебраическая и тригонометрическая формы
- •Арифметические действия с комплексными числами в тригонометрической форме.
Вычисление определенных интегралов с помощью вычетов.
Пусть функция f(z) регулярна в области D, за исключением конечного числа точек zk принадлежит D, к = 1, … ,n непрерывна вплоть до границы , за исключением тех же точек. Граница области D предполагается состояoей из конечного числа кусочно гладких ограниченных контуров. Тогда
где граница обходится в положительном направлении (т. е. при движении по границе в направлении интегрирования область D остается слева).



Интегральное преобразование Лапласа
Преобразование Лапласа - интегральное преобразование, связывающее функцию F(p) комплексного переменного (изображение) с функцией f(x) действительного переменного (оригинал).
Преобразованием Лапласа от функции f(x) (оригинала) называется функция:
![]()
f(x) называют оригиналом преобразования Лапласа, а F(p) - изображением преобразования Лапласа. f(x) и F(p) однозначно определяются друг относительно друга, тоесть если Вы знаете f(x), то всегда можете узнать F(p), и наоборот, если знаете F(p), то всегда можете получить f(x).
Оригиналы и изображения.

Свойства преобразования Лапласа, теоремы линейности, теорема дифференцируемости оригинала.
Тот
факт, что F(p) есть изображение f (t), будем
символически записывать так:
![]()
1. Линейность. Для любых комплексных постоянных a и b
![]()
(здесь и далее считать f(t)=F(p), g(t)=G(p)).
2.Теорема подобия. Для любого постоянного a >0
![]()
3. Дифференцирование оригинала. Если функции f (t), fў (t) , fІ (t),…, f (n)(t) являются функциями-оригиналами и f(t)=F(p), то
![]()
![]()
![]()
где
под f(k)(0),
(k= 1, 2,…, n-1) понимается
![]() .
.
4. Дифференцирование изображения. Дифференцирование изображения сводится к умножению на (-t) оригинала
![]()
5. Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р, т. е. если f(t)=F(p), то
![]()
6.
Интегрирование изображения. Если
интеграл
![]() сходится, то он служит изображением
функции
сходится, то он служит изображением
функции
![]()
7.Теорема смещения. Если f(t)=F(p), то для любого комплексного р0
![]()
8.Теорема запаздывания. Если f(t)=F(p), то для любого t >0
![]()
9.Теорема единственности
Если две функции j(t) и j(t) имеют одно и то же L-изображение F(p), то эти функции тождественно равны.
Теоремы затухания, дифференцирования по параметру, подобия и затухания.
Определение.
Пусть функция f (x,
![]() )
двух переменных определена для всех
значений х в промежутке [a, b] и всех
значений
во множестве
)
двух переменных определена для всех
значений х в промежутке [a, b] и всех
значений
во множестве
![]() и
при каждом постоянном значении
из
и
при каждом постоянном значении
из
![]() функция f (x,
)
интегрируема в промежутке [a, b] в
собственном или несобственном смысле.
Тогда интеграл
функция f (x,
)
интегрируема в промежутке [a, b] в
собственном или несобственном смысле.
Тогда интеграл
![]() (72)
(72)
является функцией переменной или параметра и называется интегралом, зависящим от параметра.
Основные свойства интеграла, зависящего от параметра:
Теорема 1. Если функция f(x, ) определена и непрерывна как функция от двух переменных в прямоугольнике [a, b, c, d], то интеграл (72) будет непрерывной функцией от параметра l в промежутке [c, d].
Дифференцирование по параметру под знаком интеграла.
Теорема
2. Пусть функция f(x,
)
и частная производная
![]() непрерывны в прямоугольнике
непрерывны в прямоугольнике
![]() .
В этом случае существует производная
.
В этом случае существует производная
![]() ,
которая определяется по формуле
,
которая определяется по формуле
![]() (73)
(73)
Интегрирование по параметру под знаком интеграла.
Теорема 3. Если функция f(x, ) непрерывна по переменным х и в прямоугольнике , то имеет место следующая формула:
![]() (77)
(77)
В формуле (77) пределы интегрирования a и b не зависят от параметра .
36 и 37. Операционный метод решения обыкновенных диф. уравнений и систем.
ẍ+a1ẋ+a2=f(t); a1 и a2 – постоянная
По Коши:

38. Восстановление оригинала по изображению. Оригинальный метод.
Этот метод состоит в следующем: изображение преобразовывается к удобному виду (чаще всего это изображение преобразовывается на дроби, а затем с использованием св-в преобразования Лапласа и таблиц преобразования Лапласса находят оригинал).
39. Обратное преобразование Лаппласа. Теорема обращения.
f(t)=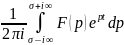 – теорема обращения.
– теорема обращения.
f(t)<Meαt p=σ+is

40. Восстановление оригинала с использованием теоремы разложения.
f(t)= ,
если t≥0
,
если t≥0
f(t)=0 t<0 ak-особые точки функции F(p)
41. Системы обыкновенных диф. уравнений. В нормальном виде. Линейная система диф. ур-ний (неоднородная).
Диф.
ур-е в нормальном виде:
Линейная сист. диф. ур-й (неоднородная):

Если fi(t)=0 – однородная система.
Если
fi(t) 0
– неоднородная система.
0
– неоднородная система.
42. Линейные однородные диф. ур-я с пост. Коэффициэнтами. Решение этих систем. Характеристическое уравнение.

ẋ=AX+F x=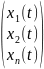 ;A=
;A= ;F=
;F= ;F=0
;F=0
Решение системы:
x1=α1ekt ẋ1=kα1ekt
x2=α2ekt ẋ2=kα2ekt
xn=αnekt ẋn=kαnekt

Делим
на ekt
и переносим:

Должно выполняться – оперделитель равен 0:
 =0
– характерестическое уравнение.
=0
– характерестическое уравнение.
Хар-е ур-е имеет ровно n различных и действительных корней.
X1= X2=
X2= Xn=
Xn=
Общее решение однородной системы:
X=
43. Устойчивость решений однородных диф.ур. Устойчивость по Ляпунову.
 - неустойчивая.
- неустойчивая.
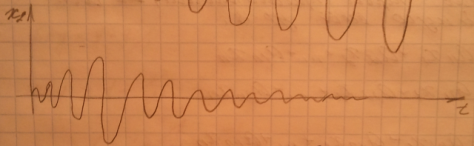 - устойчивая.
- устойчивая.
Xk(t)
 >0
>0
 >0
|xk(0)|<
>0
|xk(0)|< |xk(t)|<
|xk(t)|< ,
xk(t)
,
xk(t)
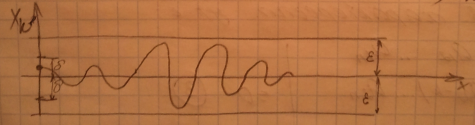
Если при этом xt стремится к 0, при t стремящимся к бесконечности, то точка называется ассимтотически устойчивой.
44. Устойчивость по первому приближению. Теорема об асимптотческой устойчивости и неустойчивости по первому приближению. Теорема Гурвица.

Составим первое приближении. Составим линейную сист. ур-й:
Теория об асимптотич. Устойчивости и неустойчивости по первому приближению:
 =0
=0
Если действ. части всех корней характеристического ур-я отриц-ны, то точка покоя сист-мы асимптотически устойчива. Если хотябы 1 из корней характеристического ур-я имеет положительную действит-ю часть, то точка покоя сист-мы не устойчива.
Теорема Гурвица. xn+a1xn-1+a2xn-2+…+an-1x+an
 - матрица Гурвица.
- матрица Гурвица.
Для того, чтобы все корни многочлена имели действ. и отрицательные части, необходимо и достаточно, чтобы они были положительными
