11. Понятие конфортного отображения

Любое преобразование плоскости в плоскость, обладающее эти свойством (т.е. свойством сохранения углов), называется конформным. Если при этом сохраняется направление отсчёта углов, то преобразование называетсяконформным преобразованием первого рода; если направление отсчёта углов меняется на противоположное, то преобразование называется конформным преобразованием второго рода. Мы доказали, что аналитическая в некоторой области G функция w = f(z) осуществляет конформное отображение первого рода во всех точках, в которых производная отлична от нуля.

П. конформного отображения второго рода – недифференцируемая функция

11. Элементарные функции комплексного переменного: ez, sin z, cos z

Показательная функция:

Наряду с введенным обозначением для показательной функции используют обозначение exp z.

Заметим, что на вещественной оси показательная функция комплексного переменного совпадает с показательной функцией действительного переменного. Непосредственная проверка убеждает, что на показательную функцию комплексного переменного переносится теорема сложения

Показательная функция комплексного переменного является периодической функцией с основным периодом 2pi, т. е.

.

3. Тригонометрические функции:

Для тригонометрических функций сохраняются теоремы сложения, а следовательно, и остальные формулы, справедливые для тригонометрических функций действительного переменного. Они являются периодическими функциями с теми же периодами, что и соответствующие тригонометрические функции действительного переменного.

Однако в случае комплексного переменного функции sinz, cosz ограниченными не являются.

11. Степенная функция

Как и в случае вещественной переменной, определим сначала степенную функцию целой сте­пени. Ниже мы покажем, как определить произвольную степень, используя логарифм и показа тельную функцию.

Определение 1. Произведение числа z на себя раз называется п ой степенью числа z

и обозначается

Свойство 1 Функция определена и непрерывна на комплексной плоскости,.

Свойство 2. Для любых справедливо

Отметим, что отображение не является инъективным. Действительно, точки и имеют одинаковые образы под действием если и Однако,

отображение является однолистным в секторах

11. Гиперболические функции

О. Функции гиперболического синуса и гиперболического косинуса комплексного аргумента определены тождествами

С. Для всех справедливы тождества

С. Функции sh z и ch z определены и непрерывны на всей комплексной плоскости.

С. Нули функций sh z и ch z лежат на мнимой оси, более того

О. Функции гиперболического тангенса th z и гиперболического котангенса cth z определены тождествами

C. функция th z непрерывна на всей комплексной плоскости за исключением точек z=iπ(k+1/2), k принадлежит Z. Функция cth z непрерывна на всей комплексной плоскости за исключением точек z=iπk k принадлежит Z.

11. Логарифмическая функция

О. Логарифмической функцией комплексного аргумента z называется функция обратная к

В силу определения.

С. Логарифмическая функция комплексного аргумента определена на всей комплексной плоскости кроме z=0 и принимает конечное число значений

C. Для всех z₁, z₂ принадлежащих С отличных от нуля, имеет мест тождество Ln(z₁*z₂)=ln z₁ +ln z₂

11. Обратная показательная функция

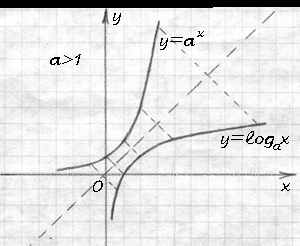
11. Обратные тригонометрические и гиперболические функции.

11. Гармонические функции

Уравнение Лапласа: ∆U≡U_xx+U_yy+U_zz=0, в полярный координатах

Функции U=U(x,y) на плоскости и U=U(x,y,z) в пространстве, имеющие непрерывные частные производные второго порядка и удовлетворяющие, соответственно, уравнению Лапласа в некоторой области D, называются гармоническими в этой области. Простейшими примерами гармонических функций являются линейные функции: U = ах + by + с на плоскости и U = ax + by + cz + d в пространстве.