
- •В 1947 г. Данцил предложил численный метод решения задачи линейного программирования - симплекс-метод.
- •Транспортная задача
- •- И при этом обеспечить минимум суммарных затрат на перевозку
- •Требуется найти какой план перевозок (набор 15 чисел) для которого выполнены все ограничения и при этом суммарная стоимость всех перевозок минимальна.
Задача 2
График занятости персонала. Экономическая модель
Имеется 7 бригад рабочих, А,Б,В,Г... С некоторым начальным распределением числа рабочих по бригадам. Задана дневная оплата работника. Задан режим работы работников:
5 дней подряд работают - 2 выходных.
Известно требуемое число работников на предприятии по дням недели. Хозяин предприятия хотел бы знать сколько работников следует нанять в каждую бригаду, чтобы обеспечить требуемое число работников по дням недели в каждый день, но при этом чтобы суммарная З/П работников оказалась минимальной.
Математическая модель
Выберем в качестве математической модели задачу математического программирования. В качестве целевой функции возьмем функцию суммарной зарплаты всех работников за неделю. Эта функция зависит от вектора х состоящего из 7 переменных:
Х1 - количество работников в бригаде А
Х2 - количество работников в бригаде Б
Х2 - количество работников в бригаде В
... и т.д.
Ограничения на переменные Х1, х2, х3...х7.
1. Число работников в каждой бригаде дб не отрицательно.
2. Число работников в каждой бригаде дб целым.
3. Число работников работающих на предприятии в каждый день недели дб не меньше чем требуется.
Нужно определить, компоненты вектора х, для которых выполнены все ограничения и для которых значение целевой функции минимально (f min). Ответом задачи является 8 чисел: 7 чисел - количество работников по бригадам, восьмое число - суммарная зарплата всех работников за неделю.
Замечание:
Поскольку суммарная зп вычисляется как произведение ежедневной оплаты одного работника на число рабочих, а общее число работников определяется суммой всех работников из разных бригад, то зависимость целевой функции линейно зависит от переменных х1, х2, х3,.....,х7, т.е. задача является задачей линейногопрограммирования.
Метод решения - симплекс-метод. Это численный метод решения систем линейных алгебраических уравнений.
Аналитический метод решений линейных алгебраических уравнений был впервые предложен в 1939 Кантаровичем.
Названия: Метод раскроя, задачи осмесси, задача о станках, транспортные задачи. (Сколько единиц продукции следует перевезти от каждого производителя до каждого потребителя, чтобы удовлетворить заказ потребителя и не превысить производственные возможности производителя и в то же время минимизировать транспортные расходы).
В 1947 г. Данцил предложил численный метод решения задачи линейного программирования - симплекс-метод.
Программное обеспечение
microsoft office
надстройка/поиск решения (с применением сиплекс-метода)
Задача 3
Транспортная задача
Экономическая модель
Имеется три завода производителя выпускающие однородную продукцию и 5 складов нуждающихся в этой продукции. Склады оформили свои заказы на продукцию. Мощности заводов известны. Известна также матрица стоимости единицы груза от каждого завода до каждого склада. Требуется составить оптимальный план перевозок. Т.е. Определить сколько единиц груза нужно перевезти от каждого завода до каждого склада с тем, чтобы
- удовлетворить заказы складов
- не превысить мощности заводов
- И при этом обеспечить минимум суммарных затрат на перевозку
Математическая модель
Выберем в качестве математической модели задачу линейного программирования. Целевая функция - это функция суммарных затрат на перевозку всех грузов. Является функцией 15 переменных и зависит от них линейно - сумма произведений на количество грузов перевезенных по данным направлениям.
Ограничения на переменные значение хij должны быт целыми (вагоны, контейнеры, бочки), не отрицательным, сумма числа грузов перевезенных с каждого завода не должна превышать его мощности, сумма всех грузов доставленных на каждый склад не должна быть меньше заказов.
Х11 х12 .....х15
Х21 х22 .....х 25
Х31 х32 .....х35
- количество единиц груза перевеззные с Iго завода нв Jый склад.
Требуется найти какой план перевозок (набор 15 чисел) для которого выполнены все ограничения и при этом суммарная стоимость всех перевозок минимальна.
Программное обеспечение
Ексель, надстройка поиск решения в режиме использования симплекс- метода.
Зачение: нельзя решать задачу методами не линейного программирования и также нельзя решать задачу не линейного программирования симплекс-методом, можно получить неправильный ответ.
Оветом является товет из 16 чисел : 15 планов перевозок и 16е минимальная стоимость всех перевозок.
11.01.13
обзор математических пакетов
российские: мезазал
Бывают:
- специализированные - используют математический аппарат 2-3 разделов математики
- универсальные - включают в себя математический аппарат по широкому классу математических методов.
Специализированные пакеты:
Axiom,
Theorist,
Derive,
Maxima(Maxyma?)
Универсальные:
MathCad - математический пакет среднего уровня ориентированный на выполнение численных расчетов на получение Числового ответа при решении экономических и инженерных задач,
Maple - ориентирован на выполнение аналитических расчетов, включает в себя большой набор программ для численного решения задач, хороший графический редактор.
Mathematica
Mathlab
первый процессор символьных вычислений был изобретен в 1980 году. Выполняет символьные выЧислитель, в канадском университете, позднее отуда вышла программа. maple - в 1995 вошла в 100 лучших программ мира, когда вышла программа для виндоус.
Общий принцип устройства пакетов:
Есть ядро символьных вычислений, в которое включены все функции, правила работы с этими функциями
Приложения - для Maple: linalq, linearAlgebra, stats, student, . Приложения создаются специалистами данной области, это позволяет использовать самые последние научные достижения в данных узких областях. С другой стороны - специалисты привыкли использовать свои собственные обозначения, поэтому одни и те же названия функций могут в разных приложениях иметь разные смыслы, и наоборот. (Maximize, minimize) !нужно обращаться к справке, получать оттуда дополнительную информацию о синтаксисе функции. Справки обычно имеют живые примеры, которые можно скопировать в рабочий документ и вставить.
Набор задач для Mathcad.
микроэкономике1. Равновестная цена
микроэкономика2. Гравитационная модель поведения потребителя
макроэкономика3. Межотраслевой баланс
макроэкономика4. Линейная модель международной торговли
Задачи для Maple:
простейшие приемы прогнозирования1. Сплайды
простейшие приемы прогнозирования2. Метод наименьших квадратов
модель конкуренции рынка. 3. Модель конкуренции: хищник-жертва
16.01.13
Математический пакет Mathcad - решение не линейный уравнений.
Речь идет о следующе задаче:
Поставновка задачи
Дано не линейное уравнение вида F(x)=0, xпринадлежит отрезку [a,b]. Требуется выЧистиль все корни, с точностью все уравнения (1) расположенные на отрезке [a,b].
Очень распростаненная математическая модель в экономических задачах и задачах управления. Речь идет о пакете Mathcad.
Геометрическое пояснение
Это те точки, в которых график пересекает ось х
Точность епселент: это значит, что корень r лежит на отрезке длина которого 2 епселент.
Математическая модель: равновестная цена и гравитационная модель
Равновесная цена.
Заданы функции спроса D(Q) и спроса предложения S(Q). Требуется выявить равновестную цену, по которой продавец согласен продать свой товар, а покупатель согласен купить его.
Равновестна цена определяется точкой, в которой функции S и D пересекаются. S(QРавн) = D (Qравн).
Q - количетсво товара в стоимостных единицах
Отыскание Qравн это уравнение
S(Q)-D(Q)=0
F(Q)=0
таким образов задача вычисления равновесной цены сводится к решению уравнения на некотором отрезке.
Способы в Mathcad
решение нелинейный уравнения в MATHcad
Solve - позволяет аналитически решать уравнение
root - численное нахождение решение одиночного корня. Следует задать значение корня приближенно.
polyroots - позволяет вычислить корни от алгебраического многочлена. Для того, чтобы получить информацию о синтаксисе этих команд нужно набрать имя команды, выделить его левой мышкой и нажать F1 и попадаем в соотвествующую страницу справки. Для вычисления корней есть два вычислительных блока
Given...Find
Given...Minerr
Given ключевое слово, набирается в рабочей области
Find - заключительная команда
Given
F(x)жир=0
Find(x)->
Если Существует готовая аналитическая формула, то пакет выдаст точный ответ записанный через радикалы
Если аналитического решения не существует, то никакой информации не будет выдано. В этом случае необходимо обратиться к численным методам решения уравнений. Для этого в начале нужно будет присвоить начальное значение корню(обычно из графического представления)
Х:=...
Given
f(x)жир=0
Find(x)=
пакет должен выдать численный ответ
В любой случае вычисление проводится с некоторой точностью, которая установлена по умолчанию, чтобы ее узнать нужно набрать:
TOL=
и пакет выдаст ту точность, которая зада паетом. Ее можно изменить, задать, но для этого ее надо задать перед обращением к вычислительному блоку
TOL:=... (До Х:=..)
Для того, чтобы узнать каким методом решается задача нужно выделить левой кнопкой мыши слово Find, в выпавшем подменю найти команду Nonlinear, кликнуть по ней, и тогда появится перечень из трех методов.
Флажок можно переставить и найти решение другим методом. Если решения совпадают до какого-то числа знаков, то можно надеяться что решение найдено верно.
Переписать!
какие задачи позыоляет решить задачу аналитически, а какие нет
Аналитическое решение нелинейный уравнений
Уравнение вида ax+b=0, => x= -b/a
P1(x)=0
Pn(x)=a0+ a1x+a2x^2+...+anxn
N=2
N=3
a0+a1x+a2x^2=0, r1=.., r2=..
P2(n)=0
Формулы Кардано
n=3->r1,r2,r3
N=4 -> правило позволяющее свести эту задачу к n3
Формула Феррари
N= 5 - не существует
при это не существует аналитических формул, которые выражали бы корни уравнения через радикалы от коэффициентов(корней) уравнений
Следует обращаться к численным методам.
В математических пакетах Mathcad и Maple уже при n=>4 используются численные методы для решения нелинейных уравнений
Интерационные методы
F(x)=0, xпринадлежит[a,b
идеи методов: чтобы вычислить корень строится/вычисляется числовая последовательность х1,х2,х3,...,хn сходящуюся к этому корню, при n->бесконечности
limXn=r
n->беск.
, обрывая последовательность на некотором элементе получает приближенное значение корня.
rПриблизит =xn
r=xn-+Е
Если Е<=епселент, то задача решена
r=xn-+Е(епселент)
Гравитационная модель поведения потребителя
Х - точка притяжения
М - человек
Предполагается, что один и тот же ТЦ действует на разных потребителей одинаково, если она находятся на одинаковом расстоянии от него. Т.е. сила притяжения зависит только от расстояния, на котором находится этот центр, и от некоторой характеристики самого центра.
Притягательность центра можно описать с помощью некоторой константы. Предположения, при которых будет строиться модель.
Математическая модель
Кц.- коэффициент привлекательности центра Ц
R- расстояние от цента до м
Сила притяжения на потребителя центра Fц.м=Кц/R^2
Экономическая модель
Дано два притягательных центра находящихся на расстоянии друг от друга
Требуется описать поведение потребителя в окрестности этих центров, С известными коэффициантами притяжения.
Математическая модель
Имеется два центра A и B. Выберем числовую осе и направим ее от центра А к центру В. Пусть Ка - коэффициент притягательности центра А
Кв - коэффициент притГательности центра В
Задача отискания нелинейного уравнения
16.01.13
Задача 5
Межотраслевой баланс
Это макроэкономическая задача.
Предположим что у нас есть несколько отраслей народного хозяйства.
Промышленность
Сельское хозяйство
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
как зависит вектор выпуска от тех потребностей, которые имеются в данном обществе (от вектора конечного спроса).
Предположим что через Y мы выделили вектор конечного спроса
Оказывается можно построить матрицу умножая которую на вектор спроса можно получить вектор выпуска.
А(тильда)*Y=x (вектор выпуска)
Y:=100
150
120
сколько продукции должна выпустить каждая отрасль, для того чтобы обеспечить вектор спроса Y
ответ дает А(тильда)*Y=x
матрица строится по таблице межотраслевого баланса. (В примере на странице 125 приведены выкладки по построению матрицы A(тильда), там она называется AEinv
Задача 6
Линейная модель международной торговли.
Экономическая модель
Имеется группа стран которые торгуют только друг с другом.
И при этом каждая страна полностью тратит свой национальный доход на покупки как у себя в стране, так и в других странах.
Какому условию должны удовлетворять нац доходы стран для того, чтобы эта система была сбалансирована.
I. II. III. IV
I. a11 a12 a13. a14
II. a21
III. a31
IV. a41
Пусть даны 4 страны
aij - доля нац дохода, в которой i-тая страна тратит на закупки в j-той стране
а11 страны которая тратит на закупки в самой себе
в пакете маткад нумерация индексов строк и столбцов по умолчанию начинается с нуля, поэтому если необходимо сохранить привычные школьные обозначения, нужно в самом начале рабочего документа написать команду
ORIGIN:=1
условия юаланса (линейная матрица удовлетворяет ли условиям сигмаV^<1> <---=1
условия которому должен удовлетворять вектор Х (состоит из доходов стран й,2,3,4. Он должен удовлетворять следующему условию - умножая матрицу А на вектор х, мы получаем этот же вектор.
АХ=1*Х
Весь нац доход страна тратит на закупки, как у себя, так и заграницей.
Лямбда=const
собственным вектором матрицы А соотвествующим собственным значением лямбда называется любой не нулевой вектор удовлетворяющий условию АХ=1*Х
Задача отискания собственного вектора Х в матрице А
Команда eigenvec(tor)(A,1)=
если матрица не удовлетворяет сумме столбцов=1
18.01.13
Универсальные математический пакет первично ориентированный наполучение точного аналитического ответа, но в то же время имеет большой набор программ для численного решения прикладных задач.
Принцип устройства пакета - модульный, у него есть центральное ядро символьных вычислений и много различных приложений по разным разделам математики. Имеет хорошую графику.
Общий недостаток математических пакетов ему присущ - в разных приложениях для одних и тех же функций используются одинаковые имена и одна и та же функция может в разных приложениях использоваться с различным синтаксисом. Нужно активно пользоваться справкой.
Fib ->New->Work seet mode
>restart; (;-конец строки)
>with ( имя приложения E);
>help (имя функции, команды);
Задача 1
Приближение таблично заданной функции интерполяционными сплайнами
I. Пусть функция y=y(x) задана таблицей
x0 |
x1 |
x2 |
... |
xn |
y0 |
y1 |
y2 |
... |
yn |
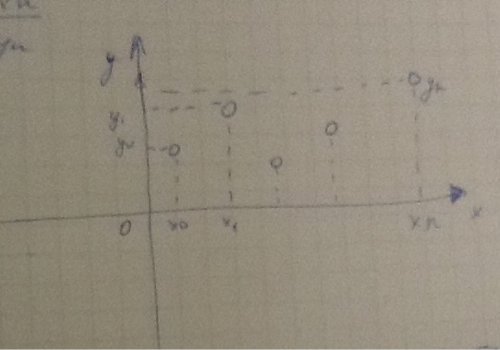
Мы хотим узнать значение этой функции, при x которого нет в таблице
Решение этой задачи происходит через теорию приближений.
основная идея - таблично заданную функцию заменяют некоторой другой функцией простого вида (обычно алгебраический многочлен), и вместоискомого. значения функции у берут значение приближающей функции.

Приближающую функцию обычно исходя из 1-2 принципов
- интерполяция - говорят, что функция фи(х) интерполирует таблично заданную функцию у(х), если [ФИ(Хк)=Ук, к=0,n.]* Т.е. Если график функции Фи(Х) проходит через заданные точки. Этим принципом разумно пользоваться, если табличное значение известно с большой точностью. Точки Хк - узлы интерполяции, а условия * - условия интерполяции.
- наилучшего среднеквадратичное приближение - метод наименьших квадратов. Применяется если исходные табличные значения заданы не точно.
Приближающую функцию в виде алгебраического многочлена обычно используют при степени к не выше n, многочлены используют при к<=7, оказывается что степень алгебраического многочлену равна k=n-1 (это утверждение теоремы Лагранжа о существовании единственного решения задачи интерполяции). Не больше 8 точек.
Если число точек велико, ( в экономике это и сотни, и тысячи точек), то используется интерполяционные сплайны.
Сплайн - Это кусочно S(x) полиномиальная функция,те функция составленная из отрезков многочленов одной и той же фиксированной степени,"сшитых" в узлах соединений.
Интерполяционный сплайн - это сплайн график которого проходит через таблично заданные точки И "сшитые" в узлах интерполяции из отрезков многочлена.
Нпример, можно построить линейный сплан-из многочленов первой степени(отдельных линий). Ели сплайн составлен из сшитых порабл, то получается квадратичный сплайн. Если сплан получен из многочленов 3 степени, те сшит из кубических порабл, то его называют кубический сплайн.
Кубический сплайн - функция S3(X) называется кубическим сплайном, если она удовлетворяет 3м условиям:
S3(X) составлена из многочленов тертьей степени на каждом из отрезк
Задача2
Модель конкуренции"Х-Ж"
экономическая модель
Рассмотрим следующую простую задачу
Имеются две популяции особей конкурирующих друг с другом
1. будем считать, что каждая встреча хищника с жертвой кончается смертью жертвы
2. Считается, что и жертва и хищники размножаются по своим законам, с разными коэффициентами, при этом чем больше "пищи", тем больше скорость размножения особей. И чем больше число особей данного вида, тем быстрее этот вид размножается
3. Нет ограничений на пищу для жертв
4. Жертвы и хищники естественной смертью не умирают
математическая модель
Влки могут "есть" бескочно
в качестве моделИ выбереМ Задачу Коши для системы двух обыкновенных дифференциальных уравнений
уравнения вальтера лотка
23.01,13
Системы комплексной автоматизации управления предприятием
Системы - позволяют оперативно получать достоверную информацию и осуществлять обратную связь, руководства организации с работниками. Системы предназначены для: сбора информации, анализа, выработки рекомендаций для работы организации. Любая система СКАУП стоит дорого, поэтому прежде чем заказывать ее, необходимо выявить те стороны работы организации, которые в первую очередь нуждаются в автоматизации и примерно оценить стоимость внедрения той или иной СКАУП. Все системы имеют модульный принцип устройства "коробочный". Те они состоят из некоторого количества контуров, каждый из которых состоит из отдельных модулей выполняющих определенные функции. В зависимости от материальных возможностей предприятия можно приобрести и установить тот или иной набор контуров. Контур бухгалтерии имеется во всех системах, также контур логистики и управление кадрами (з/п).
"1С: предприятие" (Www.1s.ru
- бухгалтерия
- логистика и склад
- Зарплата и кадры
Кроме этой системы Российского производства есть еще "Парус" (www.parus.ru) и "Галактика" (www.galaktika.ru).
стоимость системы включает в себя:
- стоимость оборудования
- стоимость наладки оборудования и согласованного между собой программного обеспечения
- стоимость обучения персонала предприятия по работе с этой системой
- стоимость Обновления ПО
Т.о. конечная стоимость может оказаться гораздо больше стоимости внедрения системы.
Процесс внедрения:
- формирование потребностей организации (нанятая комиссия или дирекция организации).
- приглашение комиссии диллеров системы (3-5 человек), которая производит анализ состояния системы управления предприятием и формирует предложение для дирекции предприятия и оценивает примерную стоимость внедрения. В результате внедрения любой системы руководство предприятия получает возможность оперативно руководить работой любых отделОв.
Иностранные ПО:
J.K. Edwards One World (www.edwards.ru)
Oracle
Sap
Microsoft Dynamics 4.0(Navision "AXAPTA")
математич модель
Экономич модель
Методы решения
Пакет обработки
