Лекция 29. Ряды с положительными членами План

1. Первый признак сравнения сходимости рядов в форме неравенств

2. Первый признак сравнения в предельной форме

3. Второй признак сходимости рядов

4. Признаки Коши и Даламбера сходимости рядов с положительными членами

5. Интегральный признак Коши-Маклорена

1. Первый признак сравнения сходимости рядов в форме неравенств

Дальше рассматриваются ряды с положительными членами:

₍₁₎

_Пусть - последовательность усеченных сумм ряда _{. Поскольку (1) - это ряд с положительными членами, то последовательность} является монотонно возрастающей, а потому она будет сходящейся тогда и только тогда, когда будет ограниченной сверху. Из этого вытекает

Теорема 1 (критерий сходимости рядов с положительными членами). Для того, чтобы ряд (1) с положительными членами сходился, необходимо и достаточно, чтобы последовательность усеченных сумм этого ряда была ограниченной сверху.

_{Теорема 2 (первый признак сравнения в форме неравенств). Пусть есть два ряда (обозначим их} и ) с положительными _{членами:}

_{, (5)}

₍₇₎

_{Если, начиная с некоторого номера} для выполняется неравенство:

(10)

то:

1. _{Из сходимости ряда} вытекает сходимость ряда ;

2. _{Из расходимости ряда} вытекает расходимость ряда .

_{Доказательство. В условии теоремы сказано, что неравенство (10) для элементов рядов} и выполняется, начиная с некоторого номера , но, учитывая то, что сходимость (расходимость) ряда не меняется, если из него удалить конечное количество элементов, можно считать, что неравенство (10) выполняется для .

Пусть - последовательность усеченных сумм ряда ; - последовательность усеченных сумм ряда .

1. Пусть ряд сходится. Из предыдущей теоремы вытекает, что тогда ограничена сверху, т.е. существует такая постоянная , что : . Учитывая неравенство (10), имеем:

для ,

т.е. последовательность усеченных сумм ряда также является ограниченной сверху, а потому ряд сходится.

2. Пусть ряд расходится. Предположим, что при этом ряд является сходящимся, тогда из доказанного в пункте 1) из этого предположения будет вытекать, что - сходящийся. Получили противоречие, поэтому наше предположение является ошибочным, а ряд - расходящимся.

2. Первый признак сравнения в предельной форме

Теорема 3 (первый признак сравнения в предельной форме). _{Пусть есть два ряда} и с положительными _{членами. Пусть существует}

(20)

тогда ряды и ведут себя одинаково, т.е. или одновременно сходятся, или одновременно расходятся.

Пример. _{Исследовать на сходимость ряд . Построим последовательность усеченных сумм этого ряда:}

.

Поскольку ,

то данный ряд является расходящимся. Расходимость этого ряда можно установить еще одним способом, пользуясь первым признаком сравнения в предельной форме, что мы и сделаем. Ряд _{называется гармоническим рядом. Этот ряд является расходящимся (это будет доказано позднее). Исходный ряд}

_.

_{Сохраняя обозначения, введенные в теоремах 2,3:}

_;

_.

_{Вычислим}

.

Таким образом, ряды и ведут себя одинаково, т.е. расходятся, поскольку о гармоническом ряде мы знаем, что он расходящийся.

3. Второй признак сходимости рядов

_{Теорема 4 (второй признак сравнения). Пусть есть два ряда (5) и (7) -} и _{с положительными членами. Если, начиная с некоторого номера} для выполняется неравенство:

(25)

то:

1. _{Из сходимости ряда} вытекает сходимость ряда ;

2. _{Из расходимости ряда} вытекает расходимость ряда .

Доказательство. Будем считать, как и раньше, что неравенство (25) выполняется для :

, , ... , , ...

Перемножим эти неравенства почленно:

. (30)

Из неравенства (30) и первого признака сравнения в форме неравенств имеем:

.

.

4. Признаки Коши и Даламбера сходимости рядов с положительными членами

Теорема 5 (признак Коши в форме неравенств). Пусть рассматривается ряд с положительными членами:

_{Построим для членов ряда} последовательность следующим образом:

. (40)

Если начиная с некоторого номера для выполняется неравенство:

,

где , то ряд сходится. Если начиная с некоторого номера для выполняется неравенство:

,

то ряд расходится.

Доказательство. Поскольку , то . Рассмотрим ряды: и ряд . Ряд - это сумма геометрической прогрессии со знаменателем , поэтому этот ряд сходится. Тогда по первому признаку сравнения в форме неравенств сходится и ряд .

Если , то , это означает, что для ряда не выполняется необходимое условие сходимости, поэтому он является расходящимся.

Теорема 6 (признак Коши в предельной форме). Рассматривается ряд с положительными членами, для которого _{построена} последовательность : . Обозначим:

.

Если , то ряд сходится, если , то ряд расходится, если , то никакого вывода о сходимости ряда сделать нельзя.

Теорема 7 (признак Даламбера в форме неравенств). Пусть рассматривается ряд с положительными членами _{Построим для членов ряда} последовательность следующим образом:

. (50)

_{Если, начиная с некоторого номера} для выполняется неравенство:

,

где , то ряд сходится. _{Если, начиная с некоторого номера} для выполняется неравенство:

,

то ряд расходится.

Доказательство. Самостоятельно.

Теорема 8 (признак Даламбера в предельной форме). Рассматривается ряд с положительными членами, для которого _{построена} последовательность : . Обозначим:

.

Если , то ряд сходится, если , то ряд расходится, если , то никакого вывода о сходимости ряда сделать нельзя.

Замечание. Во всех случаях, когда признак Даламбера дает ответ на вопрос о поведении ряда, ответ также может быть получен с помощью признака Коши. Наоборот в общем случае не верно: признак Коши более сильный, чем признак Даламбера.

Пример. Исследовать на сходимость ряд _{. Попробуем решить этот вопрос с помощью признака Даламбера.}

_.

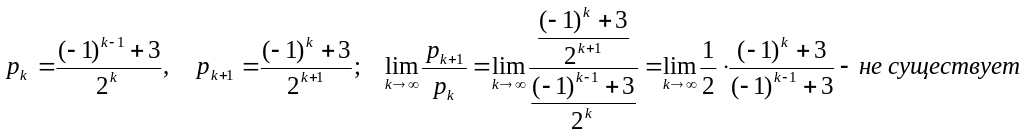_{Таким образом, признак Даламбера не дал ответ на вопрос о сходимости (расходимости) ряда.}

_{Воспользуемся признаком Коши, поскольку он более сильный, чем признак Даламбера.}

_.