Решение:

В качестве события выступает неисправность какого-то элемента. Вероятность p⁽ⁱ⁾(t) исправности i-го элемента в течение времени t определяется формулой

(2),

т.е. , , ,

где λ₁ = 1/t₁ = 1/10 = 0,1[час^-1],

λ₂ = 1/t₂ = 1/20 = 0,05 [час^-1],

λ₃ = 1/t₃ = 1/25 = 0,04 [час^-1].

Вероятности исправности элементов по истечении времени t_отк = 15 часа будут равны соответственно

, , ,

Вероятность того, что за время T i-й элемент выйдет из строя, является

противоположной вероятностью p⁽ⁱ⁾(T) :

= 1− p⁽¹⁾ (T) ≈ 1− 0,2231 = 0,7769,

= 1− p⁽²⁾ (T) ≈ 1− 0,4724 = 0,5276.

= 1− p⁽²⁾ (T) ≈ 1− 0,5488 = 0,4512.

Учитывая, что элементы работают независимо друг от друга, найдём вероятность того, что в интервале времени [0, 5] откажут:

а) только один элемент;

.

7Б. Испытывают три элемента, работающих независимо друг от друга. Длительность времени безотказной работы элементов распределена по показательному закону и равна t₁, t₂, t₃ [час]. Найти вероятность того, что в интервале времени [0, t_отк] откажут:

б) не более 2-х элементов;

7. t1 = 10; t2 = 20; t3 = 25; tотк = 15.

Решение:

В качестве события выступает неисправность какого-то элемента. Вероятность p⁽ⁱ⁾(t) исправности i-го элемента в течение времени t определяется формулой

(2),

т.е. , , ,

где λ₁ = 1/t₁ = 1/10 = 0,1[час^-1],

λ₂ = 1/t₂ = 1/20 = 0,05 [час^-1],

λ₃ = 1/t₃ = 1/25 = 0,04 [час^-1].

Вероятности исправности элементов по истечении времени t_отк = 15 часа будут равны соответственно

, , ,

Вероятность того, что за время T i-й элемент выйдет из строя, является

противоположной вероятностью p⁽ⁱ⁾(T) :

= 1− p⁽¹⁾ (T) ≈ 1− 0,2231 = 0,7769,

= 1− p⁽²⁾ (T) ≈ 1− 0,4724 = 0,5276.

= 1− p⁽²⁾ (T) ≈ 1− 0,5488 = 0,4512.

Учитывая, что элементы работают независимо друг от друга, найдём вероятность того, что в интервале времени [0, 15] откажут все три элемента:

.

11а 12а  14а   13а 15а 16а  19а 20а 26а

11а Рассматривается система с дискретными состояниями и дискретным временем (цепь Маркова). Задана матрица вероятностей перехода за один шаг. Требуется:

а) построить размеченный граф состояний;

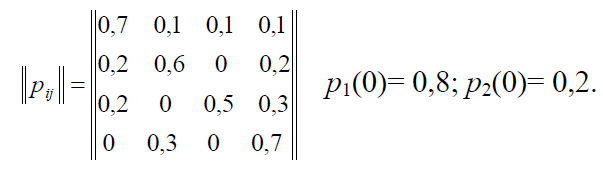
12а Рассматривается система с дискретными состояниями и дискретным временем (цепь Маркова). Задана матрица вероятностей перехода за один шаг. Требуется:

а) построить размеченный граф состояний;

14а Рассматривается система с дискретными состояниями и дискретным временем (цепь Маркова). Задана матрица вероятностей перехода за один шаг. Требуется:

а) построить размеченный граф состояний;

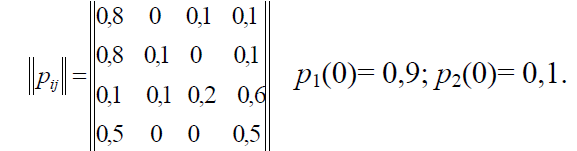
13а Рассматривается система с дискретными состояниями и дискретным временем (цепь Маркова). Задана матрица вероятностей перехода за один шаг. Требуется:

а) построить размеченный граф состояний;

15а Рассматривается система с дискретными состояниями и дискретным временем (цепь Маркова). Задана матрица вероятностей перехода за один шаг. Требуется:

а) построить размеченный граф состояний;

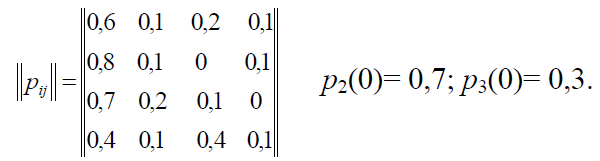
16а Рассматривается система с дискретными состояниями и дискретным временем (цепь Маркова). Задана матрица вероятностей перехода за один шаг. Требуется:

а) построить размеченный граф состояний;

19а Рассматривается система с дискретными состояниями и дискретным временем (цепь Маркова). Задана матрица вероятностей перехода за один шаг. Требуется:

а) построить размеченный граф состояний;

20а Рассматривается система с дискретными состояниями и дискретным временем (цепь Маркова). Задана матрица вероятностей перехода за один шаг. Требуется:

а) построить размеченный граф состояний;

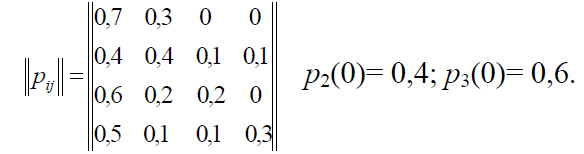
26А. Рассматривается система с дискретными состояниями и дискретным временем (цепь Маркова). Задана матрица вероятностей перехода за один шаг. Требуется составить уравнения системы для стационарного режима и найти финальные вероятности.

Уравнения системы для стационарного режима

В результате решения системы получаем значение вероятностей состояния в установленном режиме:

, , , .

37а  38а  33б   35б

35в 36в   31в 37в     

37А. Рассматривается система с дискретными состояниями и непрерывным временем. Заданы размеченный граф состояний и интенсивности переходов. Все потоки событий простейшие. Требуется:

а) составить матрицу интенсивностей переходов;

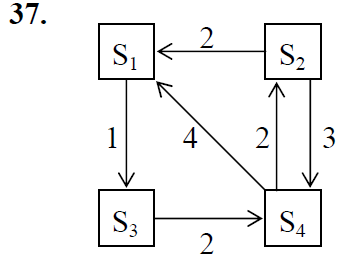
Одним из самых удобных способов является задание графа с помощью матрицы интенсивностей переходов. Задан граф G, имеющий 4 вершины S₁ S₂ S₃ S₄ и 6 рёбер. Построим матрицу 4 х 4.

Для ориентированного графа в строке, соответствующей начальной вершине дуги, ставим соответствующее число (заданное значение интенсивности) а в строке, соответствующей конечной вершине, ставим 0.

	S1	S2	S3	S4
S1	0	0	1	0
S2	2	0	0	3
S3	0	0	0	2
S4	4	2	0	0