Геометрический (графический) метод решения задачи линейного программирования
Геометрически (на плоскости) могут решаться:
задачи, заданные в произвольной форме, содержащие не более двух переменных;
задачи, заданные в канонической форме с числом свободных переменных
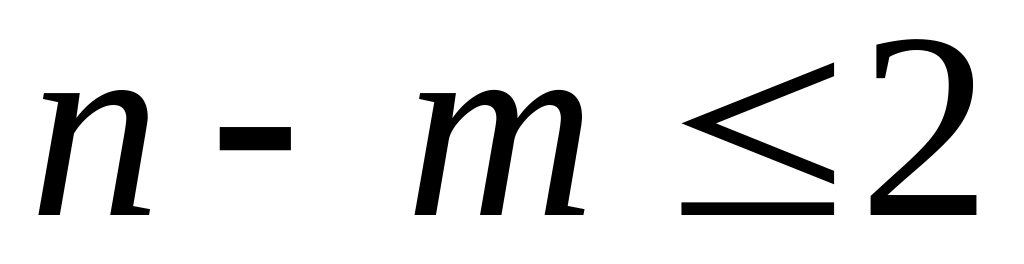;задачи общего вида, которые после приведения к канонической форме будут содержать не более двух свободных переменных.
Предварительно задача должна быть приведена к виду, в котором содержится не более двух переменных.
Решение задачи выполняется в два этапа:
построение области допустимых решений;
нахождение в области допустимых решений оптимального решения.
При построении области допустимых решений может встретиться один из трёх случаев:
пустая область;
выпуклый многоугольник;
неограниченная выпуклая многоугольная область.
|
|
|
пустая область |
выпуклый многоугольник |
неограниченная выпуклая многоугольная область |
В первом случае задача не имеет решения из-за несовместимости системы ограничений в области допустимых значений. Во втором случае задача всегда имеет оптимальное решение. В третьем, в зависимости от направления вектора коэффициентов целевой функции, задача может иметь или не иметь решения.
Если оптимальное решение существует, то возможен один из трёх исходов:
оптимальное решение единственное и совпадает с одной из вершин области;
оптимальное решение соответствует всем точкам отрезка, соединяющего две вершины области;
оптимальное решение соответствует всем точкам допустимого луча, исходящего из вершины области.
Алгоритм геометрического метода решения задачи линейного программирования
Находим
область допустимых решений системы
ограничений задачи. Строим вектор
.
Проводим линию уровня функции
или
,
которая
перпендикулярна
.
Линию уровня перемещаем по направлению
вектора
для задач на максимум и в направлении,
противоположном
,
для задач на минимум.
Направление вектора совпадает с направлением возрастания целевой функции, направление убывания целевой функции противоположно направлению вектора .
Последняя по ходу движения вершина области допустимых решений будет точкой максимума или минимума целевой функции.
Если окажется, что линия уровня параллельна одной из сторон области допустимых решений, то задача будет иметь бесконечное множество решений.
Если такой точки (точек) не существует, то делаем вывод о неограниченности целевой функции.
Определим
координаты точки максимума (минимума)
целевой функции
и вычислим значение
.
Для вычисления координат оптимальной
точки
решаем
систему уравнений прямых, на пересечении
которых находится
.
Задача. Для производства двух видов изделий А и В используются три типа технологического оборудования. Для производства единицы изделия А оборудование первого типа используется в течение 1 часа, оборудование второго типа – 3 часа, оборудование третьего типа – 3 часа.
Для производства единицы изделия В оборудование первого типа используется в течение 2 часов, оборудование второго типа – 3 часа, оборудование третьего типа – 1 час.
На изготовление всех изделий предприятие может использовать оборудование первого типа не более чем 32 часа, оборудование второго типа – 60 часов, оборудование третьего типа – 50 часов.
Прибыль от реализации единицы готового изделия А составляет 4 денежные единицы, а изделия В – 2 денежные единицы.
Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации.
Решение.
Пусть
–
количество выпускаемых изделий А;
– количество
выпускаемых изделий В.
Тогда
целевая функция
.
Ограничения задачи обусловлены временем использования оборудования, неотрицательностью объемов производства. Таким образом, математическая модель этой задачи имеет вид
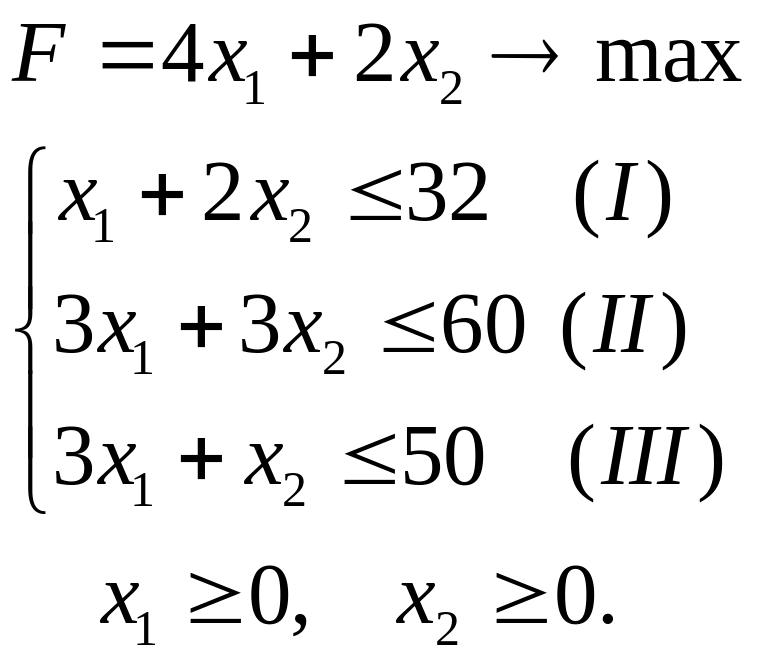
Найдем оптимальное решение задачи об использовании оборудования графическим методом.
Построим
на плоскости прямые ограничений, вычислив
координаты точек пересечения этих
прямых с осями координат, и линию уровня
.
x2
16
5
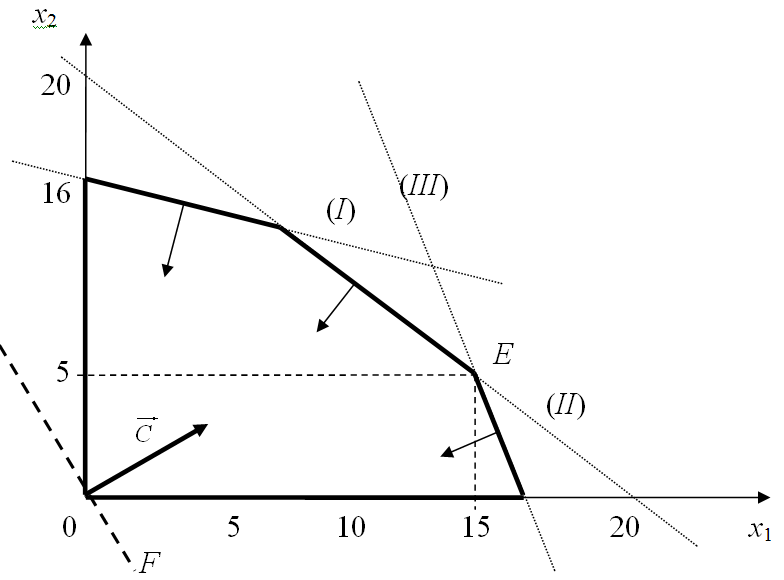
Строим
вектор
из точки (0;0) в точку (4;2). Точка Е –
последняя вершина многоугольника
допустимых решений, через которую
проходит линия уровня, двигаясь по
направлению
вектора
.
Поэтому Е
– это точка максимума целевой функции.
Определим координаты точки Е
из системы уравнений прямых (II)
и (III),
пересечением которых она является:
.
.
Максимальное значение функции равно
.
Таким образом, наилучшим планом производства изделий А и В является производство изделия А в количестве 15 единиц, изделия B – в количестве 5 единиц. Максимальная прибыль от реализации изделий А и В составит 70 денежных единиц.
Геометрический метод решения прост, нагляден, позволяет быстро и легко получить ответ, но применять его можно только в том случае, когда число переменных в стандартной задаче равно двум.
Следовательно, необходимы аналитические методы, позволяющие решать задачи линейного программирования с любым числом переменных и выявлять экономический смысл входящих в них величин.