Статистическая детерминированная модель с дефицитом

В рассматриваемой модели будем полагать наличие дефицита. Это означает, что при отсутствии запасаемого продукта, т.е. при спрос сохраняется с той же интенсивностью , но потребление запаса отсутствует – , вследствие чего накапливается дефицит со скоростью .

,

где – время, в течение которого производится потребление запаса,

– время, когда запас отсутствует и накапливается дефицит, который будет покрыт в момент поступления следующей партии.

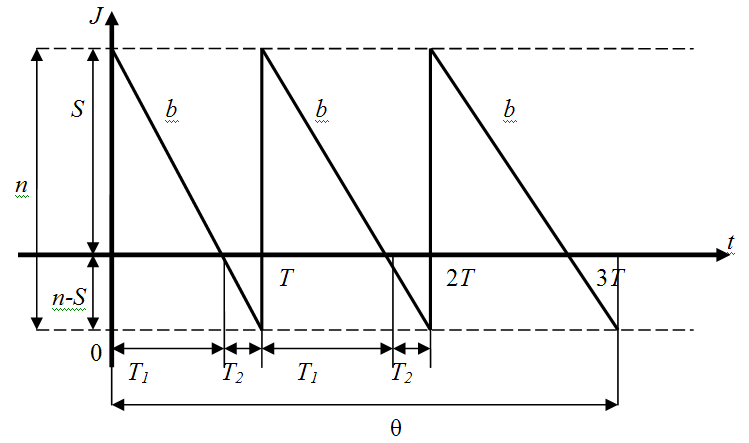
О тметим, что убывание графика ниже оси абсцисс характеризует наличие дефицита.

Необходимость покрытия дефицита приводит к тому, что максимальный уровень запаса в момент поступления каждой партии не равен её объёму , а меньше на величину дефицита .

, .

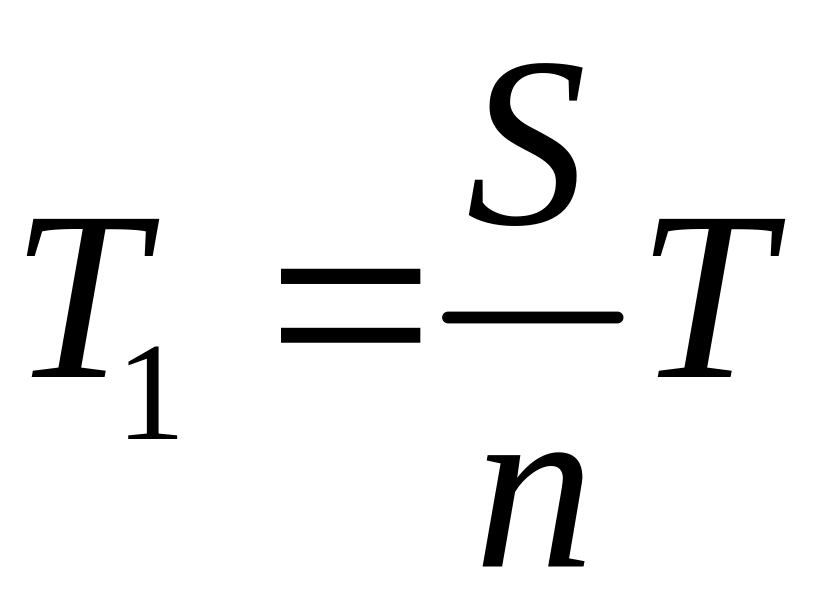Функция суммарных затрат для данной модели наряду с затратами на пополнение запаса и на хранение запаса будет включать затраты на штраф из-за дефицита :

.

Затраты 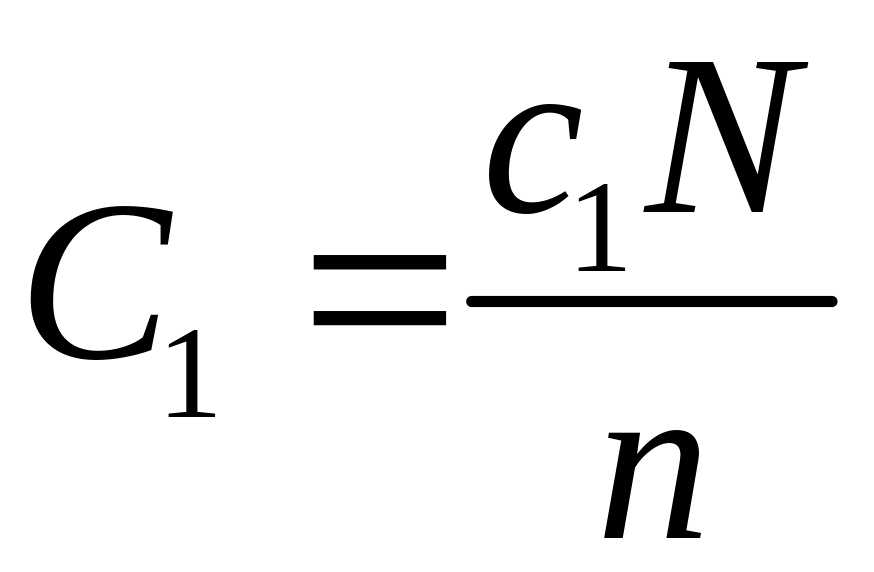. Затраты при линейном расходе запаса равны затратам на хранение среднего запаса, который за время потребления равен , поэтому эти затраты составят:

.

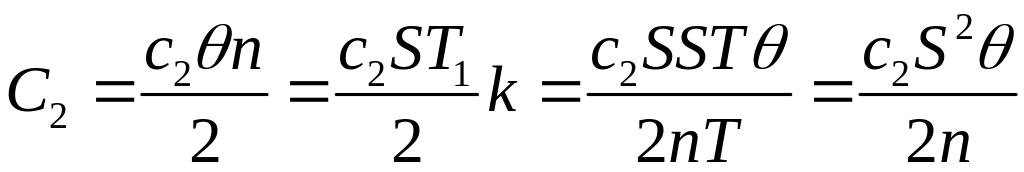При расчёте затрат будем считать, что штраф за дефицит составляет в единицу времени на каждую единицу продукта. Так как средний уровень дефицита за период равен 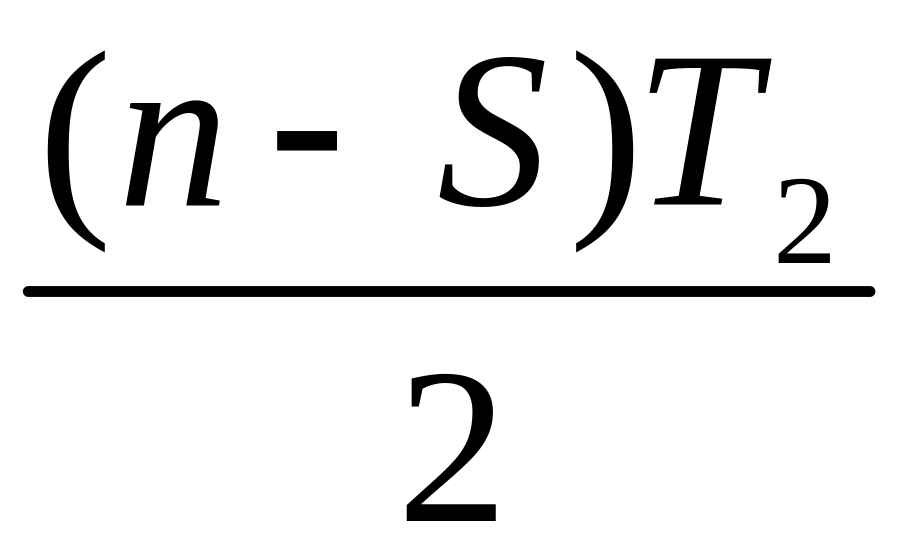, то штраф за этот период составит 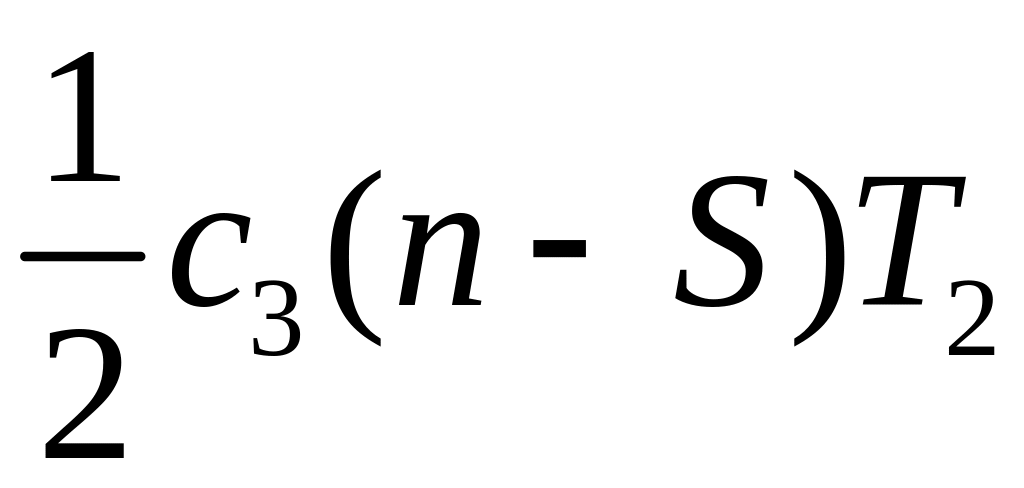, а за весь период будут равны:

.

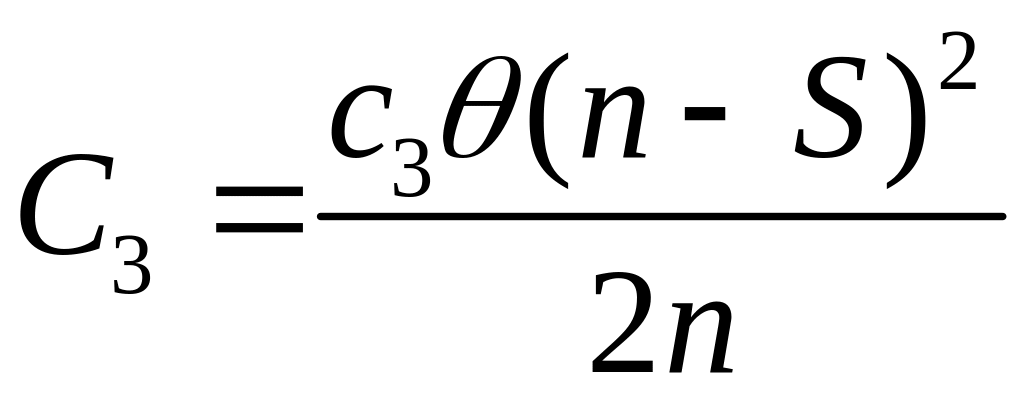Следовательно, суммарные затраты равны:

.

Замечание. При модель совпадает с предыдущей моделью управления запасами без дефицита.

Задача управления запасами с дефицитом сводится к отысканию такого объёма партии и максимального уровня запаса , при которых функция принимает минимальное значение. То есть необходимо исследовать функцию двух переменных на экстремум.

Приравнивая частные производные , к нулю, получим после преобразования систему уравнений:

Решая систему, получаем формулы наиболее экономичного объема партии и максимального уровня запаса для модели с дефицитом:

,

.

Замечание. С помощью достаточного условия экстремума можно доказать, что функция при , достигает минимума.

Величина 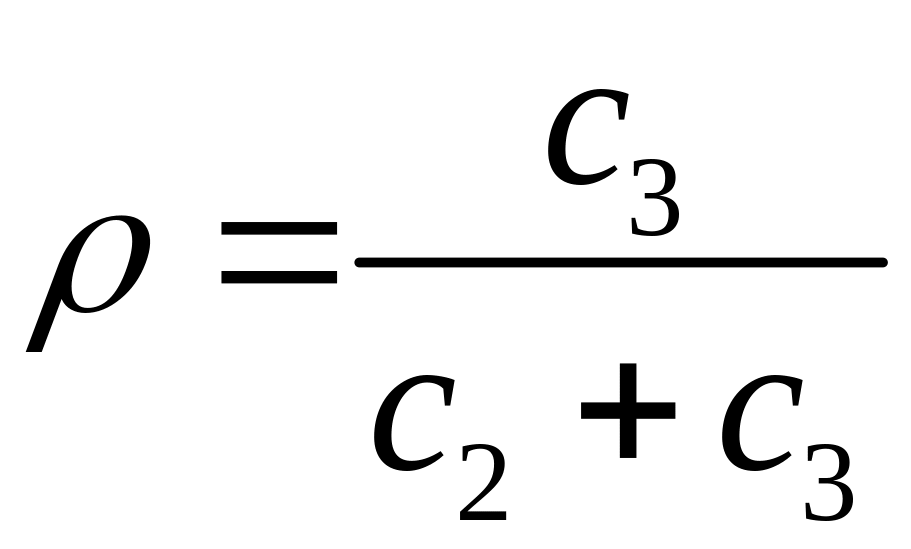называется плотностью убытков из-за неудовлетворённого спроса.

Если значение мало по сравнению с , то величина близка к нулю; если значительно превосходит , то близка к единице.

Недопустимость дефицита равносильна предположению о том, что или что Итак, формулы наиболее экономичного объема партии и максимального уровня запаса для модели с дефицитом:

, .

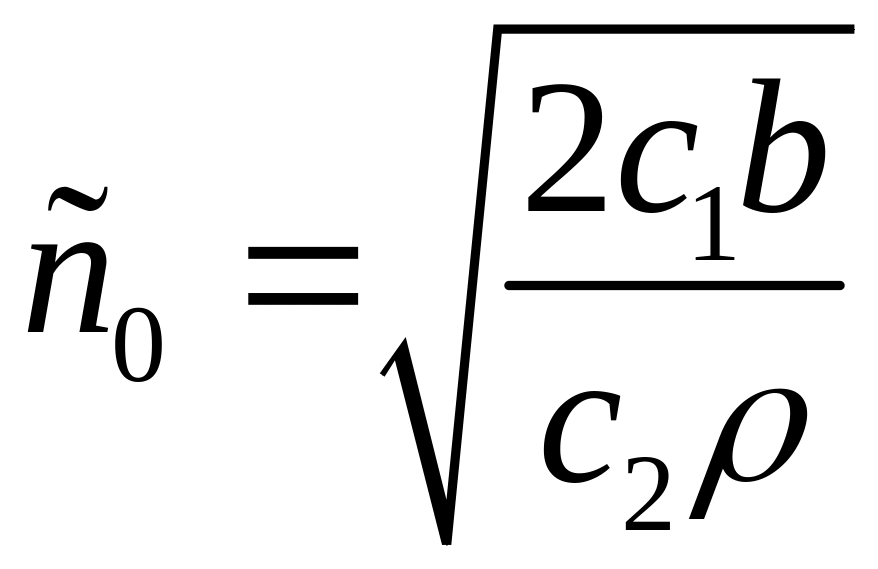Оптимальные объёмы партии для задач с дефицитом и без дефицита при одинаковых параметрах связаны соотношением 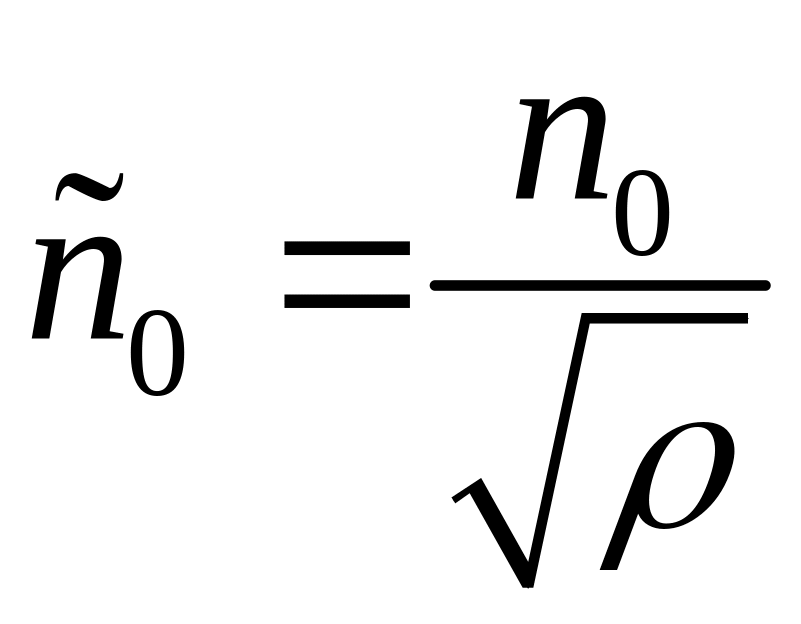, откуда вытекает, что оптимальный объем партии в задаче с дефицитом всегда больше (в раз), чем в задаче без дефицита.

Задача. Найти наиболее экономичный объём партии и интервал между поставками в условиях предыдущей задачи, если известно, что отсутствие каждой детали приносит в сутки убытки в размере 4 ден. ед.

Решение. Штраф за дефицит составляет в единицу времени на каждую единицу продукта = 4.

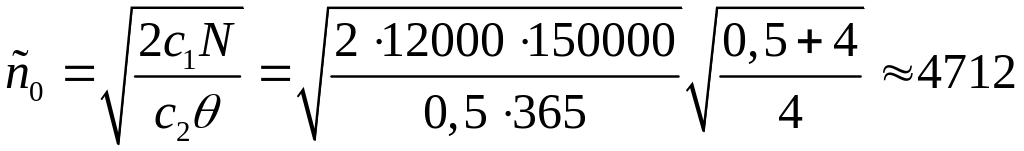деталей

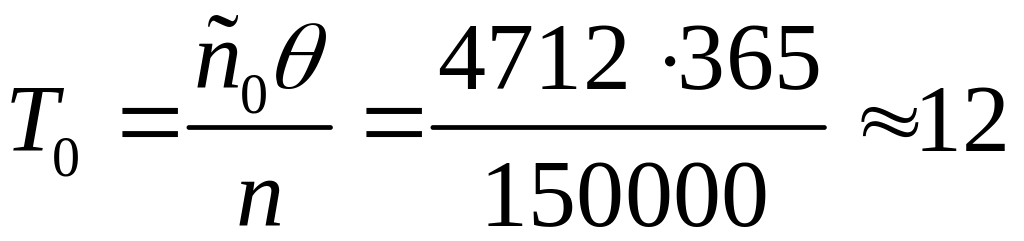дней.