Многокритериальные задачи оптимизации
На практике часто требуется найти экстремальные значения нескольких экономических показателей. В этом случае математическая модель имеет несколько целевых функций, причем некоторые из них могут требовать нахождения максимального, а другие – минимального значения.
Поэтому возникает задача нахождения такого компромиссного решения, в котором значения всех рассматриваемых экономических показателей были бы приближены к экстремальным значениям.
Нахождение компромиссного решения относится к многокритериальным задачам оценки оптимальности. Для практической деятельности подобные задачи решаются следующими способами.
Ранжированием показателей в порядке их значимости, важности. После чего приступают к поиску решения, оптимального по наиболее важному из них. Задавшись допустимой величиной изменения первого критерия, ищут решение по второму критерию, наилучшему в полученной области, и т. д. Порядок значимости и допустимые диапазоны выбирают произвольно.
Нахождением единого (интегрального) показателя эффективности посредством суммирования произведений имеющихся показателей на «весовые» коэффициенты (коэффициенты важности показателей).
Превращением всех целевых функций, кроме одной, в ограничения.
Математическая модель задачи
Дана математическая модель экономической задачи, в которой две целевые функции и система ограничений линейны. Найдем компромис-сное решение по двум показателям, один из которых требует нахождения максимума, а другой – минимума.
при
ограничениях:
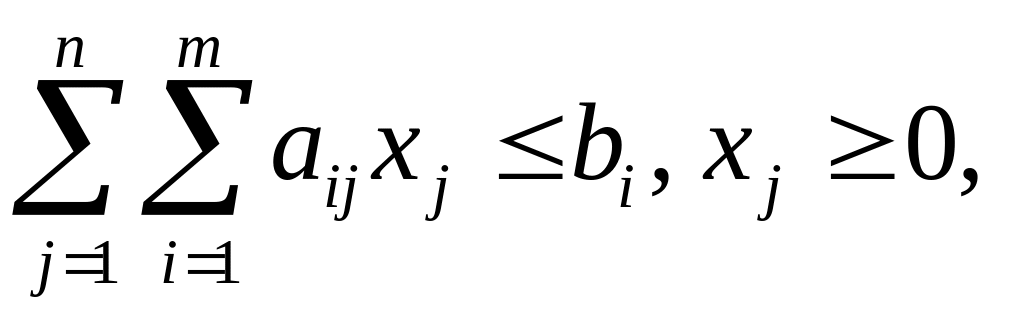
где
,
– значения
целевых функций (экономические
показатели);
– коэффициенты;
– переменные.
Решим
задачу по каждому показателю в отдельности
и найдем оптимальные значения
,
.
П
роделав
преобразования над целевыми функциями,
получим математическую модель нахождения
компромиссного решения задачи с двумя
целевыми функциями:
при ограничениях:
где
–
целевая функция;
– наибольшее относительное значение
экономических показателей.
Математическая модель будет аналогичной в случае нахождения решения задач, имеющих три и более целевые функции.
Классические методы оптимизации
Во многих экономических моделях зависимости между факторами лишь в первом приближении можно считать линейными. Такие показатели как прибыль, себестоимость, капитальные затраты на производство и т.д. зависят от объема производства, расхода ресурсов и т.п. нелинейно. Можно выделить класс нелинейных задач, которые относятся к классическим методам оптимизации. Эти методы часто используются как основа для теоретического анализа. Используя классические методы оптимизации, следует четко представлять различие между локальным экстремумом функции, глобальным экстремумом и условным экстремумом.
Многим
экономическим явлениям присуща
многофакторная зависимость, поэтому
при изучении процессов в экономике
вводят функции нескольких переменных.
Например, прибыль
,
получаемая предприятием при реализации
продукции двух видов, и объем производства
и
этих видов продукции связаны между
собой следующим образом:
,
где
,
– прибыль от реализации единицы продукции
каждого вида. В данном случае говорят,
что
– функция от двух переменных
и
,
а переменные
и
называют аргументами этой функции.
Итак,
функцией
двух переменных
называется правило, по которому каждой
паре чисел
из
некоторого множества
соответствует единственное число
,
которое обозначается
и называется значением функции
в точке
.
Область
называется областью определения функции.