2.13 Доверительный интервал для доли.

Доверительный интервал для разности долей:

Критерий z можно определить как

Разность выборочных долей

Z = -------------------------------------------------------------------

Стандартная ошибка разности выборочных долей

Величина z имеет приблизительно нормальное распределение; (z можно применять для проверки гипотезы о равенстве двух выборочных долей (или, что то же самое, для оценки статистической значимости различий выборочных долей)). Можно показать, что даже если в совокупностях, из которых извлечены выборки, доли различны, то отношение

Разность выборочных долей - Разность истинных долей

Z = -----------------------------------------------------------------------------

Стандартная ошибка разности выборочных долей

приближенно следует нормальному распределению — при условии, что объемы выборок достаточно велики.

Если р_] и p₂ — истинные доли в каждой из совокупностей, а p1 и p2 (с галочкой наверху) - выборочные оценки этих долей, то

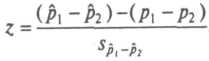
В 100(1 -а) процентах случаев z по абсолютной величине не превышает z_а, то есть

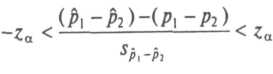
Преобразовав это неравенство, мы получим формулу для 100(1-α)-процентного интервала для разности истинных долей:

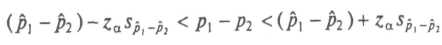
Распределение Стьюдента с увеличением числа степеней свободы стремится к нормальному. Поэтому z_аможно найти в табл. 4.1(Гланц) — в строке, соответствующей беско нечному числу степеней свободы.

Чаще всего используют 95% доверительный интервал, в этом случае z_а = z0,05 =1,96.

ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ ДОЛИ

Если объем выборки достаточно велик, то доверительный ин тервал для доли можно приближенно вычислить, используя нормальное распределение*.

Когда выборка мала (а в медицинских исследованиях так оно обычно и бывает), приближение нормальным распределением недопустимо. В таких случаях приходится вычислять точные значения доверительных интервалов, используя биномиальное распределение. Заметим, что при оценке долей по выборкам небольшого объема расчет доверительного интервала особенно желателен. Причина в том, что, если выборка мала, изменение признака даже у одного из ее членов приведет к резкому изменению долей.

Итак, при достаточно большом объеме выборки величина

Наблюдаемая доля — Истинная доля

Z = -------------------------------------------------------------------

Стандартная ошибка долей

приближенно следует нормальному распределению.

Математическая запись для z:

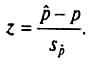
Отсюда получаем формулу для 100(1-α)-процентного доверительного интервала для истинной доли:

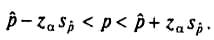
2.14. Определение необходимого объема выборки.

Логично, что неразумно стремиться к неоправданно большому числу испытаний, если убедительный результат можно получить при минимально допустимом объеме выборки. Необходимая численность выборки n, отвечающая точности, с какой намечено получить средний результат, зависит от величины ошибки выборочной средней и определяется по формуле:

где t – нормированное отклонение, s²_x– выборочная дисперсия,  - величина, определяющая границы доверительного интервала.

Допустим, провели n1=5 измерений, p=0,95 и 12,6-4,8<μ<12,6+4,8 (где 4,8 – ошибка). Ошибка слишком велика. Какой V выборки надо взять, чтобы уменьшить эту величину в 4 раза?

S не сильно изменяется при различных n (характеризует разброс вариантов самой генеральной совокупности).

(1)