Свойства матриц полного факторного эксперимента

 

Для матриц таких экспериментов характерны следующие свойства.

1. Свойство симметричности относительно центра эксперимента - алгебраическая сумма элементов столбца каждого фактора равна нулю:

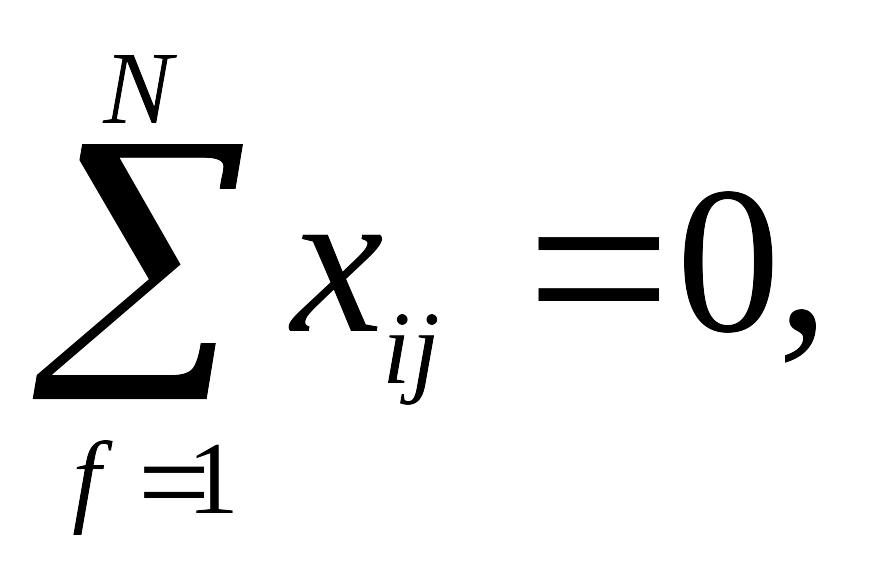
где j - номер опыта; i - номер фактора; N - число опытов в матрице.

2. Свойство нормировки - сумма квадратов элементов каждого столбца равна числу опытов:

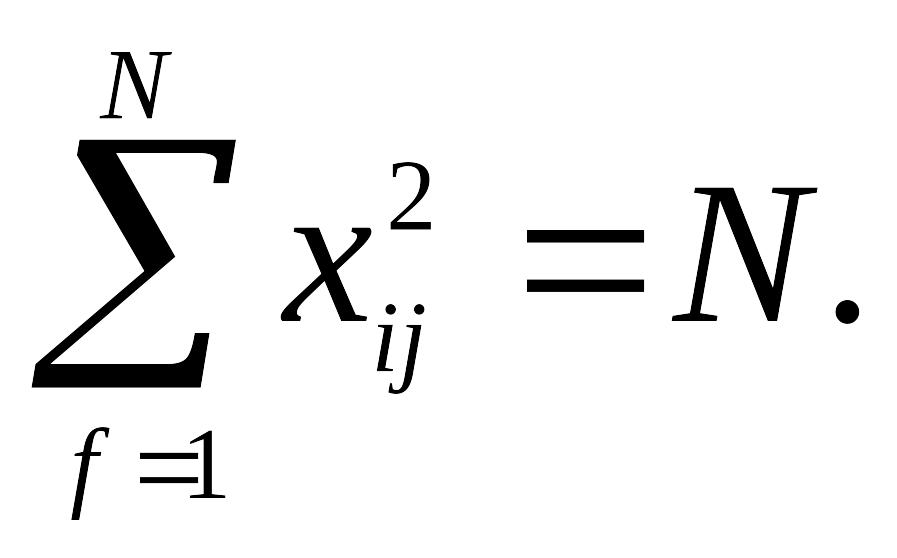
3. Свойство ортогональности - сумма построчных произведений элементов любых двух столбцов равно нулю:

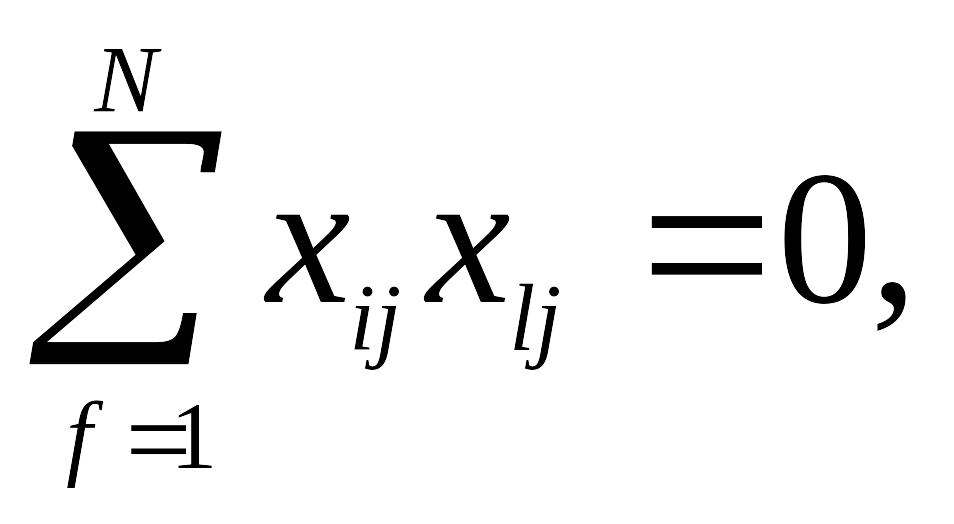
где i, l - номера факторов, причем i¹l.

Ортогональность является одним из наиболее важных свойств матрицы. Ортогональность матрицы позволяет оценить все коэффициенты уравнения регрессии независимо друг от друга, т. е. величина любого коэффициента не зависит от того, какие величины имеют другие коэффициенты. Если тот или иной коэффициент регрессии окажется незначимым, то его можно не учитывать, не пересчитывая остальных.

4. Свойство ротатабельности: точки в матрице планирования подбирают так, что математическая модель, полученная по результатам полного или дробного факторных экспериментов, способна предсказывать параметры оптимизации с одинаковой точностью в любых направлениях на равных расстояниях от центра эксперимента. Это очень важное свойство матрицы, так как, начиная эксперимент, исследователь не знает, в каком направлении предстоит двигаться в поисках оптимума.

4. 4 Дробный факторный эксперимент.

При числе опытов в полном факторном анализе, значительно превышающем число определяемых параметров модели, применяют так называемый дробный факторный эксперимент (ДФЭ), к-рый представляет собой часть плана ПФЭ. ДФЭ может содержать половину, четверть и т.д. опытов от ПФЭ.

При количестве факторов, равном 10, количество экспериментов =2¹⁰=1024. В таких случаях факторы разделяют: в 2 раза — 2⁹-512 экспериментов, в 4 и т.д. Оптимальным считается примерно 2⁴=16 экспериментов.

ДФЭ часто применяют в методе Бокса-Уилсона (метод крутого восхождения):

Выбирают начальную точку, в окрестности к-рой проводят ПФЭ или ДФЭ (в зависимости от числа факторов); по его результатам рассчитывают параметры мат. модели 1-го порядка. Если модель адекватна, с ее помощью определяют направление изменения факторов, соответствующее движению к экстремальному значению целевой ф-ции в направлении градиента или антиградиента (соотв. при поиске максимума или минимума). Движение в выбранном направлении осуществляют с помощью последовательно выполняемых опытов и производят до тех пор, пока отклик изменяется желаемым образом. В найденной наилучшей (для выбранного направления) точке снова выполняют ПФЭ или ДФЭ и т.д. Изложенную процедуру повторяют до построения адекватной модели на каждом этапе.

Позже, в 1961 году, метод немного усовершенствовали: вокруг точки (x₁, x₂), которая использовалась как начальная, наметили 4 точки, → поставили в них эксперименты, в каждой нашли отклик; по ним провели плоскость, касательную к поверхности отклика и таким образом нашли точку экстремума.