
Лабораторна робота №3 Стек
Мета роботи:
- оволодіти навичками роботи з пам'яттю в стеках;
- навчитися вирішувати завдання з використанням стеків.
Теоретичні відомості
Ключові терміни:
LІFO (Last Іnput - Fіrst Output) - це метод доступу до елементів стеку за принципом "останнім прийшов - першим вийшов";
вершина стеку - це доступний елемент стеку;
стек (англ. stack - стопка) - це структура даних, у якій новий елемент завжди записується в її початок (вершину) і черговий елемент, що, зчитується, також завжди вибирається з її початку (рис. 1).
У списках доступ до елементів відбувається за допомогою адресації, при цьому доступ до окремих елементів не обмежений. Але існують також і такі спискові структури даних, у яких є обмеження доступу до елементів. Одним із представників таких спискових структур є стековий список або просто стек.
У стеках використається метод доступу до елементів LІFO. Найчастіше принцип роботи стеку порівнюють зі стопкою тарілок: щоб взяти другу зверху, потрібно спочатку взяти верхню.
Стек - це список, у якого доступний один елемент (одна позиція). Цей елемент називається вершиною стеку. Взяти елемент можна тільки з вершини стеку, додати елемент можна тільки у вершину стеку. Наприклад, якщо записані в стек числа 1, 2, 3, то при наступному витягу одержимо 3,2,1.
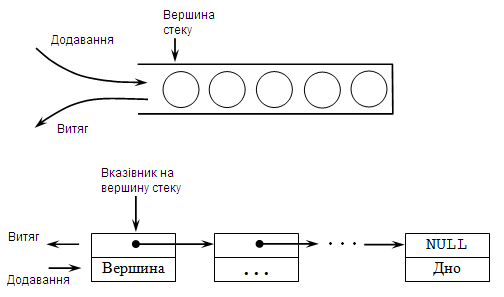
Рисунок 1. Стек и його організація
Опис стеку виглядає в такий спосіб:
struct им’я_типу {
інформаціне поле;
адресне поле;
};
де
- інформаційне поле - це поле кожного раніше оголошеного або стандартного типу;
- адресне поле - це вказівник на об'єкт того ж типу, що і обумовлена структура, у нього записується адреса наступного елемента стеку.
Например:
struct list {
type pole1;
list *pole2;
} stack;
Стек як динамічну структуру даних легко організувати на основі лінійного списку. Оскільки робота завжди йде із заголовком стеку, тобто не потрібно здійснювати перегляд елементів, вилучення і вставку елементів у середину або кінець списку, то досить використати економічний за пам'яттю лінійний односпрямований список. Для такого списку досить зберігати вказівник вершини стеку, що вказує на перший елемент списку. Якщо стек порожній, то списку не існує, і вказівник приймає значення NULL.
Опис елементів стеку аналогічний опису елементів лінійного односпрямованого списку. Тому оголосимо стек через оголошення лінійного односпрямованого списку:
struct Stack {
Single_List *Top;//вершина стеку
};
. . . . . . . . . .
Stack *Top_Stack;//вказівник на вершину стеку
Основні операції, роботи зі стеком:
- створення стеку;
- перегляд стеку;
- додавання елемента у вершину стеку;
- витяг елемента з вершини стеку;
- перевірка чи порожній стек;
- очищення стеку.
Реалізацію цих операцій розглянемо у вигляді відповідних функцій, які, у свою чергу, використовують функції операцій з лінійним односпрямованим списком. Зверніть увагу, що у функції створення стеку використовується функція додавання елемента у вершину стеку.
//створення стеку
void Make_Stack(int n, Stack* Top_Stack){
if (n > 0) {
int tmp;//допоміжна змінна
cout << "Введіть значення ";
cin >> tmp; // вводимо значення інформаційного поля
Push_Stack(tmp, Top_Stack);
Make_Stack(n-1,Top_Stack);
}
}
//друк стеку
void Print_Stack(Stack* Top_Stack){
Print_Single_List(Top_Stack->Top);
}
// додавання елемента у вершину стеку
void Push_Stack(int NewElem, Stack* Top_Stack){
Top_Stack->Top =Insert_Item_Single_List(Top_Stack->Top,1,NewElem);
}
// витяг елемента з вершини стеку
int Pop_Stack(Stack* Top_Stack){
int NewElem = NULL;
if (Top_Stack->Top != NULL) {
NewElem = Top_Stack->Top->Data;
Top_Stack->Top = Delete_Item_Single_List(Top_Stack->Top,0);
// вилучаємо вершину
}
return NewElem;
}
// перевірка чи порожній стек
bool Empty_Stack(Stack* Top_Stack){
return Empty_Single_List(Top_Stack->Top);
}
//очищення стеку
void Clear_Stack(Stack* Top_Stack){
Delete_Single_List(Top_Stack->Top);
}
Задание 2. Вычисления на стеке
Общая информация
Задание состоит из двух частей, первая из которых обязательна для выполнения, вторую необходимо выполнить для получения отличной оценки. Срок сдачи задания — 9 октября.
а. Вычисление значения арифметического выражения, заданного в инфиксной форме.
Теория
Говорят, что выражение записано в инфиксной форме, если знак операции (сложения, умножения, вычитания либо деления) стоит между своими аргументами, например, 5 + 7. Каждая операция имеет приоритет выполнения (сначала выполняются умножение и деление, затем сложение и вычитание). Для изменения приоритета выполнения операций используются круглые скобки.
Вычислять значение выражения, записанного в инфиксной форме, неудобно. Проще сначала перевести его в постфиксную, или обратную польскую запись, в которой знак операции записывается после своих операндов, например, 5 7 +.
Для перевода выражения из инфиксной формы в постфиксную с учетом приоритетов операций и скобок существует простой алгоритм (Дейкстры). Алгоритм работает со стеком, в котором хранятся знаки операций. Сначала стек пуст. На вход алгоритму подается последовательность лексем (числа, скобки или знаки операций), представляющая некоторое арифметическое выражение, записанное в инфиксной форме. Результатом работы алгоритма является эквивалентное выражение в постфиксной форме. Вводятся приоритеты операций: открывающая скобка имеет приоритет 0, знаки + и – — приоритет 1 и знаки * и / — приоритет 2.
Если не достигнут конец входной последовательности, прочитать очередную лексему.
Если прочитан операнд (число), записать его в выходную последовательность.
Если прочитана открывающая скобка, положить ее в стек.
Если прочитана закрывающая скобка, вытолкнуть из стека в выходную последовательность все до открывающей скобки. Сами скобки уничтожаются.
Если прочитан знак операции, вытолкнуть из стека в выходную последовательность все операции с большим либо равным приоритетом, а прочитанную операцию положить в стек.
Если достигнут конец входной последовательности, вытолкнуть все из стека в выходную последовательность и завершить работу.
Заметим, что порядок операндов в выходной последовательности не отличается от порядка операндов в исходной последовательности. В выходной последовательности отсутствуют скобки.
Для вычисления значения выражения, записанного в постфиксной форме, можно использовать описанный далее алгоритм. На вход подается последовательность лексем (числа или знаки операций), представляющая некоторое арифметическое выражение, записанное в постфиксной форме. Результатом работы алгоритма является значение этого выражения.
Если не достигнут конец входной последовательности, прочитать очередную лексему.
Если прочитан операнд (число), положить его в стек.
Если прочитан знак операции, вытолкнуть из стека два операнда и положить в стек результат применения прочитанной операции к этим операндам, взятым в обратном порядке.
Если достигнут конец входной последовательности, завершить работу. В стеке останется единственное число — значение выражения.
Ясно, что эти два алгоритма можно объединить, если в первом алгоритме вместо вывода в выходную последовательность передавать лексему сразу на вход второму алгоритму и обрабатывать «на лету» (придется поддерживать одновременно два стека).
Формулировка задания
Во входном файле input.txt в единственной строке находится арифметическое выражение, записанное в инфиксной форме (используются только целые положительные числа и четыре операции +, –, *, /. В выходной файл output.txt записать значение этого выражения. Стеки реализовывать при помощи связанных списков (операции добавления в начало списка и удаления первого элемента, см. теорию по заданию 1.
Примеры
Ввод: input.txt (1+2)*(3+4) |
Вывод: output.txt 21 |
b. * Выполнение программы вычислений
Формулировка задания
Во входном файле input.txt находится программа, написанная на специальном языке программирования. В языке существуют два вида операторов: оператор присваивания VARIABLE=EXPRESSION, где VARIABLE — имя переменной, состоящее из букв и цифр, не начинающееся с цифры и длиной не более 5 символов, а EXPRESSION — выражение в инфиксной форме, содержащее целые числа, скобки, знаки операций (+, –, *, /) и переменные и не содержащее пробелов. Значением любой переменной изначально считается 0, оператор присваивания изменяет значение переменной на значение выражения. Второй вид оператора — оператор вывода на экран: PRINT EXPRESSION, где PRINT — служебное слово, а EXPRESSION определяется так же, как и для оператора присваивания. Этот оператор выводит в файл output.txt значение выражения EXPRESSION и переводит строку.
