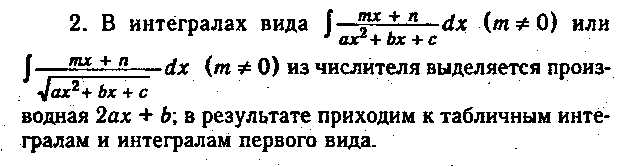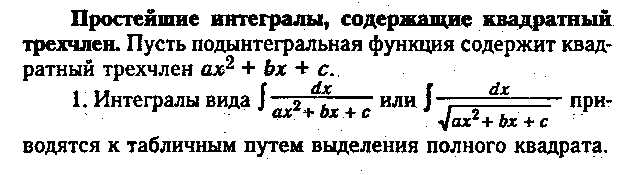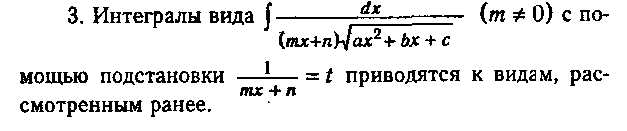17. Интегрирование некоторых выражений, содержащих квадратный трехчлен
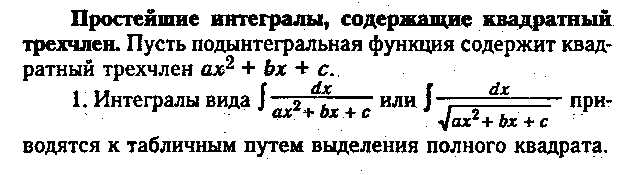
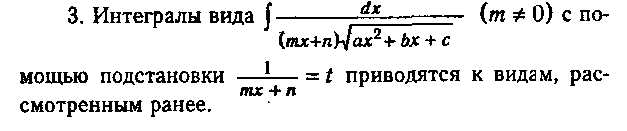
№13. Определение первообразной ф-ции и неопределённого интеграла.
Пусть ф-ии f(x) и F(x) определены на интервале (а; b). Если ф-ия F(x) имеет производную на интервале (а; b) и для всех х, принадл. (а; b) выполняется равенство F’(x)=f(x), то ф-ия F(x) наз-ся первообразной ф-ии f(x) на интервале (а; b).
Если F1(x) и F2 (x) – любые две первообразные ф-ии f(x) на интервале (a; b), то для всех х, принадл. (a; b) выполняется равенство F2(x)=F1(x)+C , где С—некоторая постоянная.
Совокупность
всех первообразных ф-ии f(x)
на интервале (a;
b)
наз-ся неопределённым
интегралом
от ф-ии f(x)
на этом интервале и обозн.
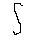f(x)dx,
т.е.
f(x)=F(x)+C
(a<x<b),
где C—произвольная
постоянная.