I стадия II cтадия III и IV cтадии

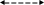
ATC_min

AVC

AVC_min

MC_min б)

AFC

0 Q

Q_C Q_B Q_A

Рис. 7.1. Издержки производства в краткосрочном периоде

Переменными называются такие издержки (VC), которые изменяются в зави­симости от объема производства. К ним относятся затраты на выплату заработ­ной платы, начисляемой в зависимости от выработки, затраты на сырье, материалы, топливо, энергию, транспортные, юридические, консалтинго­вые услуги и т.д.

Когда продукция не выпускается, переменные издержки равны нулю в то время как постоянные издержки находятся на фиксированном уровне. Однако по мере роста объема выпускаемой продук­ции VС увеличиваются, предприятию больше потребуется сырья, материалов, труда и т.д. В начальной стадии увеличения производства VС растут медленнее объема производства (до объема производства в точке С), а затем начинают увеличиваться быстрее по сравнению с ростом производства (см. рис 7.1,а).

Такой характер изменения VС объясняется действием закона убывающей отдачи, или закона убывающего предельного продукта. Пока на начальном этапе увеличения использования переменного ресурса предельный продукт возрастает переменные издержки возрастают меньшими темпами, чем объем производства (кривая VC до объема производства Q_c будет выпуклой). Но с момента уменьшения предельного продукта сумма VC будет увеличиваться быстрее, чем объем производства (кривая VC после Q_с будет вогнутой).

Сумма FС и VС дает общие издержки (ТС), которые увеличиваются по мере роста выпуска продукции. На гра­фике кривая ТС полностью повторяет кривую VС, но сдвинута от нее вверх на величину постоянных издержек, так как ТС = FC + VC.

Для принятия обоснованных управленческих решений менеджерам фирм необходимо знать не только общую сумму издержек, приходящихся на тот или иной объем продукции, но и уровень средних издержек, т.е. издержек, приходящихся на единицу продукции. Сопоставление средних издержек с ценой по конкретному продукту показывает, является ли производство продукта прибыльным или убыточным

Выделяют следующие виды средних издержек:

средние общие издержки (АТС): АТС = ТС/Q;

средние постоянные издержки (АFС): АFС = FС/Q;

средние переменные издержки (АVС): АVС = VС/Q;

Взаимосвязь между различными видами средних издержек выражается в следующей формуле:

АТС = АFС + АVС .

Своеобразным видом издержек, приходящихся на единицу продукции, являются предельные издержки. Предельные издержки (МС) - это дополнительные издержки, связанные с производством дополнительной единицы продукции. Они определяются по формуле:

МС = DТС/DQ => МС = dТС/dQ,

т. е. предельные издержки равны производной функции общих издержек по объему производства. Поскольку ТС есть сумма FС и VС, и в этой сумме FС есть величина постоянная, производная которой равна нулю, то справедлива и такая формула предельных издержек: МС=dVС/dQ.

Для фирмы стратегически важно определение предельных издержек, которые возможно полностью контролировать. С помощью предельных издержек возможно точно определить, во что предприятию обойдется расширение производства на одну дополнительную единицу и какие расходы предприятие сэкономит при сокращении производства на одну единицу.

Для решения вопросов определения оптимального объема выпуска менеджерам фирмы надо знать, как изменяются средние и предельные издержки с ростом объема производства

Средние общие издержки, также как и предельные издержки, для любых объемов выпуска могут быть определены из кривой общих затрат.

Исходя из того, что АТС = ТС/Q, средние общие издержки для данного объема выпуска равны тангенсу угла наклона луча, проведенного из начала ко­ординат и через точку на кривой ТС, соответствующую этому объему выпуска. Например, средние общие издержки в точке А, которой соответствует объем вы­пуска Q_A, составляют ТС_A/Q_A, т.е. равны тангенсу угла наклона луча 0А (рис.1 а). Этот луч в точке A касается кривой ТС.

При объеме производства Q_A в точке А средние общие издержки являются мини­мальными, потому что тангенсы углов наклона лучей, проведенных через другие точки кривой ТС, будут больше тангенса угла наклона луча ОА. Причем, при росте производства от 0 до Q_A средние общие издержки будут уменьшаться, а после Q_A - возрастать. Таким образом, кривая АТС имеет форму параболы. Это соответствует характеру изменения средней производительности переменного ресурса. Пока при увеличении объема выпуска средняя производительность растет, АТС уменьшаются, но с момента уменьшения среднего продукта АТС начинают возрастать. Точка минимума АТС совпадает с точкой максимума среднего продукта.

Подобным же образом можно описать и кривую АVС. В этом случае тан­генс угла наклона луча, выходящего из начала координат и касательного к кри­вой VС в точке В, соответствует минимальному значению АVС. Средние пере­менные издержки также описываются параболической кривой. Следует заметить, что Q_A > Q_B а это значит, что АТС становятся минимальными при большем объеме выпуска, чем АVС.

Функция средних постоянных издержек является убывающей функцией, имеющей форму гиперболы. При увеличении объема производства средние постоянные издержки снижаются и кривая АFС асимптотически приближается к оси абсцисс. Поскольку АFС с ростом объема производства стремятся к нулю, то кри­вые АVС и АТС по мере увеличения Q сближаются. Следует принять во внима­ние, что расстояние между кривыми АТС и АVС равно величине АFС.

Так как предельные издержки МС = dTС/dQ, то их величина для опреде­ленного объема продукции равна тангенсу угла наклона касательной, проведен­ной через точку на кривой ТС, соответствующую этому объему производства. Если вдоль кривой ТС провести касательные к ее точкам и проследить как изменяется тангенс угла их наклона, то получается следующее: вначале МС уменьшаются и достигают минимального значения в точке С, которая явля­ется точкой перегиба кривой ТС, а затем по мере роста производства МС возрас­тают. Таким образом, кривая МС тоже имеет параболическую форму. Это соот­ветствует действию закона убывающей отдачи: на начальном этапе роста выпус­ка, когда предельный продукт растет, МС уменьшаются, а с момента убывания предельного продукта МС возрастают. Точка минимума МС совпадает с точкой максимума предельного продукта.

Как предельные издержки соотносятся с АТС и AVC? МС = AVC тогда, когда АТС минимальны. Доказательство этого положения следующее:

выше было выяснено, что АТС минимальны, когда объем выпуска равен Q_A. При этом АТС равны тангенсу угла наклона луча ОА. Но луч ОА является касательной к кривой ТС в точке А. Поэтому тангенс угла наклона луча ОА одновременно равен величине МС. Таким образом, МС = АТС, когда АТС минимальны.

Точно так же можно доказать, МС = AVC, когда AVC минимальны.

При анализе производственной функции в краткосрочном периоде производственный процесс был представлен четырьмя стадиями. Рассмотрим эти производственные стадии с позиций поведения издержек производства в краткосрочном периоде.

Стадия I начинается от нулевого уровня выпуска до точки максимально­го предельного продукта переменного фактора. Средний продукт на этой стадии растет. С издержками на этом интервале происходят сле­дующее: предельные издержки уменьшаются и достигают минимума при максимальном предельном продукте, средние общие издержки тоже снижа­ются.

Стадия II соответствует такому уровню выпуска, при котором предель­ный продукт уменьшается, но он еще пока больше среднего продукта. Поэтому средний продукт растет и достигает максимального значения, когда сравнивает­ся с предельным продуктом. На этом интервале предельные издержки возрастают а средние общие издержки уменьшаются до тех пор пока не сравниваются с предельными издержками. В точке равенства МС и АТС средние общие издержки достигают минимума.

На Ш стадии средний продукт переменного фактора уменьшается, предельный продукт, будучи положительным, тоже уменьшается и достигает нулевого уровня. На этом интервале вместе с выпуском увеличиваются и сред­ние и предельные издержки.

На IV стадии рост производства идет при отрицательных значениях предельного продукта переменного фактора и поэтому средние и предельные издержки возрастают очень быстро. Комбинации ресурсов, характерные для этой стадии, не включаются в производственную функцию.