5. Правила контроля построения эпюр

Они вытекают из определения продольной силы N_z , поперечной силы Q_y , изгибающего момента M_x и второго уравнения равновесия элемента балки.

1. Там, где есть сосредоточенная внешняя сила, направленная вдоль оси z, на эпюре сил N_z имеет место скачок на величину этой силы.

2. Точно так же там, где есть сосредоточенная внешняя сила, направленная поперек оси z, на эпюре поперечных сил Q_у имеет место скачок на величину этой силы.

3. Аналогично, там, где есть сосредоточенный момент, на эпюре моментов есть скачек на величину этого момента.

4. Там где поперечная сила пересекает нулевую линию, там имеет место экстремум на эпюре (см. следствие в конце раздела 3.2).

6. Общий случай напряженного состояния

6.1.Нормальные и касательные напряжения

Рассмотрим брус. Разделим его на две части (см. рис.6.1)..

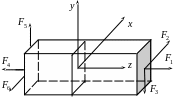
Рис.6.1.

Правая часть действует на левую в каждой точке сечения. Нарисуем это утверждение (см. рис.6.1). Введем термины для поверхностных нагрузок, которыми правая часть действует на левую:

- нормальное напряжение (напряжение растяжения или сжатия);

- касательные напряжения (первый индекс определяет рассматриваемую площадку, второй индекс указывает направление действия напряжения).

Правило знаков для : Если оно действует на сечение растягивающим образом, то оно считается положительным.

Правило знаков для : Для прочностных расчетов знак касательных напряжений не имеет значения, но для определенности введем его в соответствии с правилом, применяемым в теории упругости, то есть, касательное напряжение положительно, если оно действует в направлении оси х и при этом направление нормали к сечению совпадает с осью z.

Аналогично вводится знак касательных напряжений .

6.2. Закон парности касательных напряжений

Вырежем из тела малый элемент (рис.6.2). Со стороны соседних элементов на него кроме растягивающих напряжений действуют и касательные напряжения (рис.6.3). Рассмотрим случай, когда растягивающих напряжений нет. Поскольку все тело находится в покое, то и любая его часть, в том числе рассматриваемый малый параллелепипед также находится в покое.

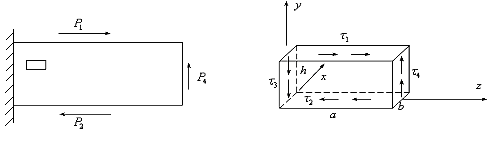
Рис.6.2 Рис.6.3

Запишем для него уравнения равновесия:

Отсюда вытекает

Закон парности можно сформулировать следующим образом.

Если на грани элемента тела возникает напряжение , то на других трех гранях также возникает такое же напряжение . При этом они сходятся к ребру или расходятся от ребра.

Примечание. Здесь мы рассмотрели случай отсутствия нормальных напряжений. Но этот закон имеет место и при их наличии. Для доказательства этого надо использовать следующие приемы.

Если вертикальные грани имеют бесконечно малый размер h по сравнению с горизонтальным, то нормальные напряжения не будут давать вклад в первое уравнение равновесия. Аналогично для второго уравнения. Для третьего уравнения можно выбрать ось х, проходящую через центр параллелепипеда.