21. Теория предельного равновесия и её использование при расчете конструкций

Основы современной теории предложил А.А.Гвоздев в 30-е годы при разработке методов расчета железобетонных конструкций. В отличие от обычного подхода теории сопротивления материалов, называемого методом расчета по рабочему состоянию на стадии упругого деформирования тела (часто именуемого также методом расчета по допустимым напряжениям), эта теория основана на использовании пластических свойства материалов и позволяет определить разрушающую нагрузку.

Основной постулат теории заключается в следующем:

Если в каком то малом элементе тела (стержня), наступает состояние, при котором начинается текучесть, то этот элемент не перестает работать, а продолжает сопротивляться с постоянным напряжением:

.

Разрушением считается состояние не разделения на части, а состояние, при котором происходит переход конструкции в механизм, то есть в состояние, при котором она уже не может удерживать дополнительную нагрузку и деформируется неограниченно. Рассмотрим некоторые примеры.

21.1. Несущая способность стержневой конструкции

Пусть плита подвешена на двух стержнях. Необходимо найти нагрузку , которую может выдержать данная конструкция.

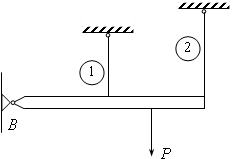
Рис.21.1

Ясно, что плита начнет неограниченно перемещаться (вращаясь около опоры) только тогда, когда оба стержня потекут. Тогда в первом стержне и во втором: .

Введем силовую схему, заменяя противодействие опоры реакциями. Проведем сечение I-I и заменим действие верхней части конструкции на нижнюю силами N₁, N₂ (см. рис.21.2).

Запишем уравнение равновесия:

: => .

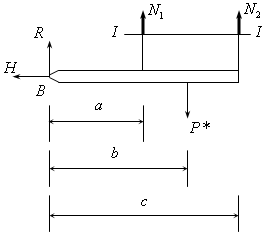
Рис.21.2

Отсюда получаем разрушающую нагрузку:

.

21.2 Задача изгиба балки Предельный момент

Рассмотрим балку (см. рис.21.3), которая изгибается силами Р и моментом т.

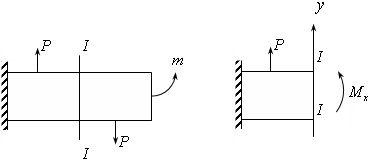
Рис.21.3

Сделаем сечение I-I. На него справа действует изгибающий момент . Нарисуем эпюру при разных значениях М_х (см. рис.21.4). При некотором достигаем состояния, при котором . Еще более увеличивая придем к тому, что нижние и верхние волокна будут пластически деформироваться при постоянном . Дальнейшее увеличение приведет к тому, что по всей высоте волокна перейдут в пластическое состояние (см. рис.21.5). Геометрически это означает, что в данном сечении изгиб балки будет не плавным, а сосредоточенным (см. рис.21.6).

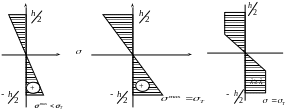
Рис.21.4

Рис.21.5 Рис.21.6

Это состояние в сечении называется предельным, сечение называют пластическим шарниром, а момент, который вызывает такое состояние, также называется предельным. Обозначают его через .

П одсчитаем его значение. Как обычно разбиваем сечение на малые площадки. Тогда:

,

.

В нашем случае . Следовательно:

Рис.21.7

Подсчитаем момент для верхней части сечения:

.

Здесь - это статический момент верхней половины сечения. Для нижней части получим то же самое. В результате:

. (21.1.)

Рассмотрим пример отыскания предельной нагрузки для статически неопределимой балки (рис.21.8).

Рис.21.8

Р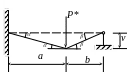 азрушение произойдет тогда, когда под силой и в заделке произойдет пластический излом.

Рис.21.9

Это означает, что под силой и в заделке момент достигает предельного значения . Найдем из закона сохранения энергии.

Работа силы будет

.

Здесь v – это прогиб под силой (см. рис.21.9). Эта работа тратится на создание пластических шарниров в заделке и под силой. Подсчитаем работу, которую совершает в них момент .

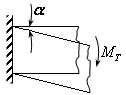
Рис.21.10

В заделке момент повернул стержень на угол , значит он совершил работу:

.

Рассмотрим теперь малый элемент под силой Р. Тогда:

, .

Закон сохранения энергии дает:

,

.

Выразим и через . Так как перемещения малы, то

, .

Значит: , .

Тогда: .

Подставляя, получаем:

.

21.3. Применение теории предельного равновесия для расчета

болтовых (заклепочных) и сварных соединений

Пусть 2 элемента соединяются болтом. Существует две опасности – срез болта и сматие пластины или болта.

А) В) С)

Рис.21.11

Разрушение срезом

Считаем, что при разрушении происходит срез болта, ввиду возникновения предельных значений касательного напряжения (рис.21.9 В).

Тогда:

.

Если болтов несколько, то получим:

. (21.2)

Теперь можно найти допустимую силу

. (21.3)

Если же дана проектная сила Р, то можно из (21.3) найти количество болтов, обеспечивающих прочность соединения.

Разрушение смятием

Разрушение может произойти в результате смятия самого болта или пластины. Пластина при этом воздействует на болт по сечению А напряжением (см. рис.21.11 С).

Тогда:

.

Расчет сварных соединений

Рассмотрим продольные швы:

Рис.21.12

Нарисуем разрушенное состояние. Из уравнения равновесия следует, что:

.

Запишем условие прочности (k - коэффициент запаса):

.

С учетом того, что отсюда получаем .

Основной задачей расчета сварных швов является определение минимально-допустимой длины шва. Выражая площадь фигуры ВСDК через l найдем:

, => .

Это расчетная длина шва. При изготовлении сварки расчетную длину увеличивают на 1 сантиметр, так как по концам шва всегда образуются микротрещины на глубину порядка 0,5 сантиметров.

Торцевые швы (или лобовые швы) рассчитываются аналогично:

.
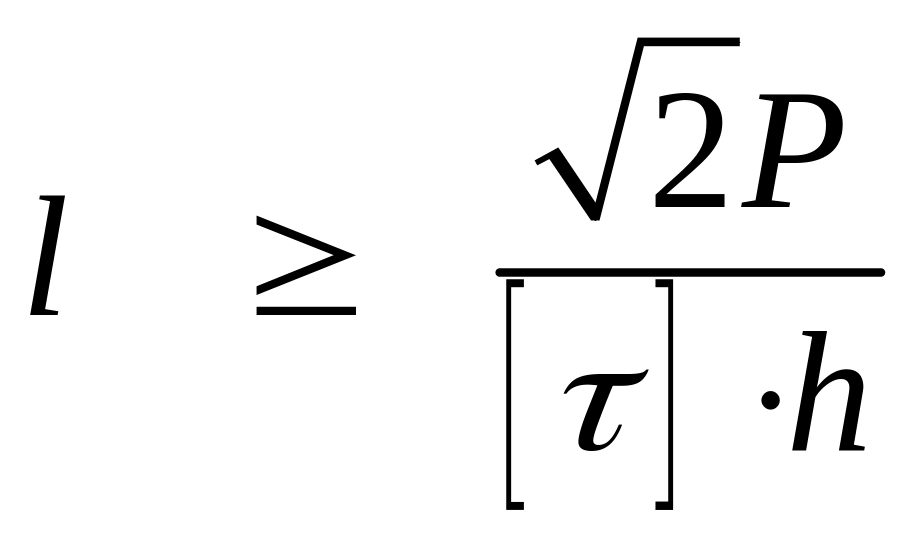