19.2. Растяжение с изгибом

Рассмотрим растяжение с изгибом (см. рис.19.3).

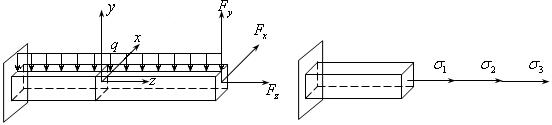
Рис.19.3 Рис.19.4

Проанализируем задачу отыскания нормального напряжения .

Ясно, что он складывается из напряжений, возникающих при растяжении ( ), при вертикальном изгибе ( ), горизонтальном изгибе ( ), т.е.:

.

Здесь , , .

Суммируя, получаем:

. (19.1)

Эту формулу иногда называют основной формулой сопромата.

З десь - это координаты точки (бесконечно малой площадки), в которой мы вычисляем .

Рис.19.5

Ясно, что из (19.1) следует ряд формул для простых деформаций:

1. Если нет изгиба, то . Тогда получим для простого растяжения: .

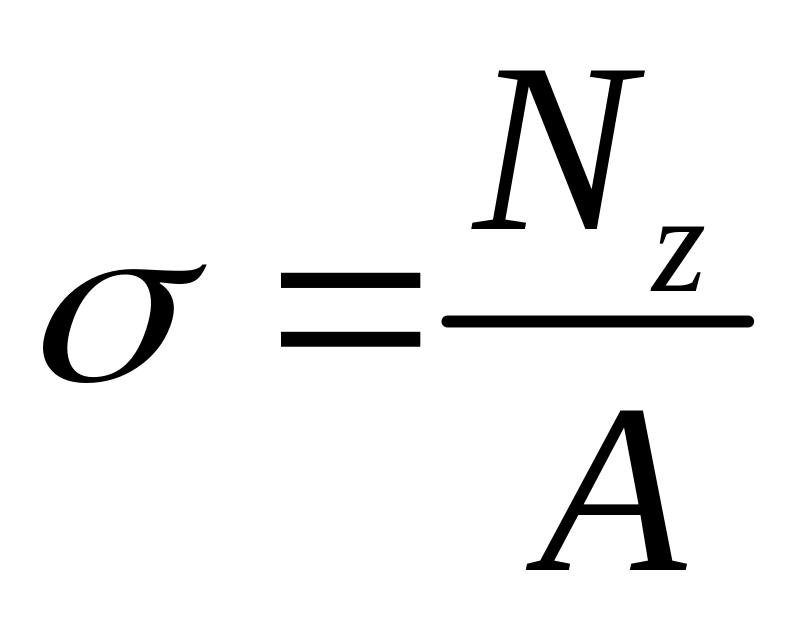2. Если нет растяжения, но 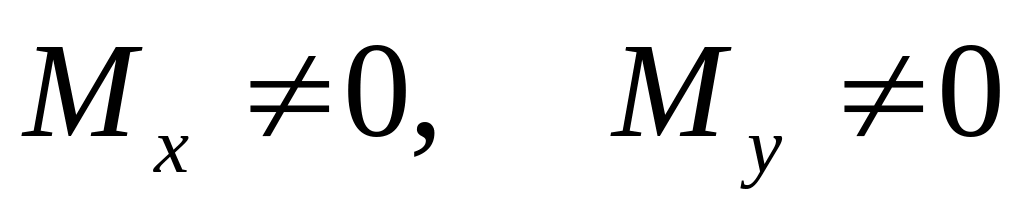, то получим для косого изгиба:

.

3. Если то получим случай прямого поперечного изгиба:

.

19.3. Максимальные напряжения при растяжении с изгибом

Из формулы видно, что в разных точках с разными напряжение разное. При расчете на прочность необходимо знать (максимальное сжимающее напряжение) и (максимальное растягивающее напряжение).

Рассуждаем от противного. Найдем сначала линию, на которой напряжение минимально, то есть .

Подставим =0 в (19.1):

. (19.2)

В данном сечении - это постоянные, поэтому уравнение (19.2) – это уравнение прямой в плоскости х,у (см.рис.19.6).

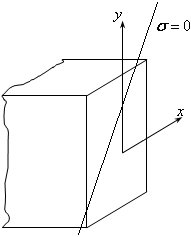
Рис.19.6

Напомним определение: прямая, на которой , называется нейтральной.

Ясно, что вблизи нейтральной линии напряжение не нуль, но очень мало. И чем дальше от этой линии, тем напряжение больше. Следовательно, , возникают в точках, наиболее удаленных от этой нейтральной линии.

Определение: точки, в которых или называются опасными точками.

Примечание. Из (19.1) видно, что в разных сечениях комбинация может давать разные комбинации и , то есть в одном сечении максимальным будет , а в другом . Более того, нельзя заранее знать, в каком сечении или будут наибольшими.

Поэтому при растяжении с изгибом опасными являются все те сечения, в которых или , или экстремальны.

19.4 Косой изгиб

Это случай сложной деформации, при котором есть только изгиб в двух плоскостях.

В этом случае в формуле (19.1), полагаем .

Тогда: .

Уравнение нейтральной линии получает вид:

.

Видно, что нейтральная линия проходит через центр тяжести.

Особенностью косого изгиба и растяжения с изгибом в общем случае является то, что нейтральная линия (штриховая прямая на рис.19.7) не перпендикулярна равнодействующей F поперечных сил F_х , F_у .

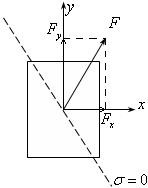
Рис.19.7

19.5. Проверка прочности круглых стержней при кручении с изгибом

Будем рассматривать только круглые стержни.

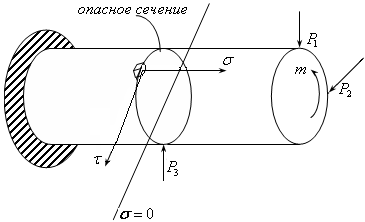
Рис.19.8

Пусть стоит задача: проверки прочности в опасном сечении. Исследуем малый элемент в опасном сечении (см. рис.19.8)

Рис.19.9

Особенность ситуации в том, что на элемент действуют два вида напряжений одновременно, поэтому условие прочности вида , , не обеспечивают прочность, поскольку они справедливы только при простом растяжении и при простом сдвиге. Так как и действуют одновременно, то в зависимости от материала, нужно применять различные теории прочности.

Для стали в запас прочности можно использовать III теорию:

. (19.3)

Здесь вычисляется как обычно: .

Для полого вала имеет вид:

. (19.4)

Для отыскания для круглых стержней не обязательно находить опасную точку. Действительно, если найдена нейтральная линия, то мы можем принять её за ось .

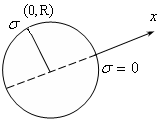
Рис.19.10

В этом случае опасной будет точка с координатами х = 0, у = R (рис.19.10). Изгибающий момент тогда вычисляется как геометрическая сумма и :

. (19.5)

Поэтому по формуле Навье найдем:

, .

Если кроме кручения и изгиба имеется растяжение, то максимальное значение напряжения вычисляется по формуле:

. (19.6)