18.7. Кручение стержней открытого профиля

Рассмотрим кручение стержней с прямоугольным сечением.

Рис.18.29

Точное решение получено Сен-Венаном. Но можно получить приближенное решение и инженерными методами, считая, что стержень – это совокупность круглых валов, как это показано на рис.18.30.

Рис.18.30

Введем систему координат (см. рис. рис.18.29). Если считать, что напряжения не меняются по ширине рассматриваемого прямоугольника, а только по высоте, то получим:

. (18.28)

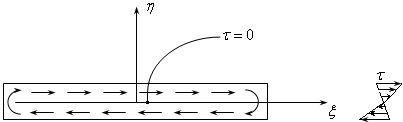
Рис.18.31

Разбив площадь на микроплощадки и вычисляя силу , которая действует на нее, можно подсчитать момент, который создает сила . Например, от горизонтальных напряжений момент будет

. (18.29)

Приравнивая сумму всех моментов крутящему моменту можно найти выражение для :

. (18.30)

Здесь: .

Формулу для теперь можно записать в виде, аналогичном случаю круглых валов (см. формулу (18.5)):

, где . (18.31)

Для угла закрутки стержня прямоугольного сечения формула имеет вид:

. (18.32)

Здесь в отличие от круглых валов (см.формулу (18.10)) в знаменателе есть коэффициент 2.

Если стержень состоит из нескольких прямоугольников (см. рис.18.16), то выкладки (18.28) – (18.31) будут такими же. Изменится только момент инерции . Он будет состоять из суммы моментов каждого прямоугольника:

. (18.33)

Сравнивая (18.31) с (18.19) можно заметить, что в отличие от тонкостенных стержней замкнутого профиля в стержнях с открытым профилем максимальные напряжения возникают там, где , т.е. там, где стенка является наиболее толстой. Значит и разрушение начнется в самом толстом месте сечения.

Отметим, что стержни с замкнутым профилем намного прочнее и жестче, чем стержни с открытки профилем. Для примера можно рассмотреть трубу квадратного сечения ширины а, постоянной толщины t (см. рис.18.28). Тогда .

Вычислим напряжение и угол закрутки для трубы с замкнутым контуром:

, .

Если же разрезать трубу вдоль оси (например, вдоль ребра), то получим стержень с открытым контуром. Вычислим максимальное напряжение (которое будет при ) и угол закрутки. Учитывая, что получим:

. .

Найдем отношения напряжений и углов закрутки , :

, .

Видно, что при малых t напряжение и угол будут гораздо больше. Например, если положить а = 20 см., t = 1мм., то получим

, .

Можно сказать, что после разреза трубы прочность понизилась в 300 раз, а жесткость в 30000 раз.

19. Сложная деформация

Сложная деформация – это совокупность двух или более простых типов деформации бруса.

Их виды:

1. Растяжение с изгибом.

2. Кручение с изгибом.

3. Кручение с изгибом и растяжением.

4. Растяжение с кручением.

5. Косой изгиб (изгиб в двух плоскостях).

19.1. Эпюры внутренних силовых факторов

Разделим брус сечением на две части. На одну часть со стороны другой в трехмерном пространстве действует 6 силовых факторов . Правила знаков для сил и моментов, действующих в плоскости xz, принимаем такими же, как и для плоскости уz (они были введены в разделе 3.1). В отличие от случая простого изгиба их эпюры строятся в аксонометрии (или в изометрии), причем, обычно эпюры изображаются на отдельных рисунках, эпюры - на одном отдельном рисунке, - также на одном отдельном рисунке.

Пример: Рассмотрим L-образную балку (рис.19.1). На каждом участке ось z направляется вдоль стержня, а оси x,y-перпендикулярно стержню. При этом систему x, y, z желательно передвигать как жесткое целое.

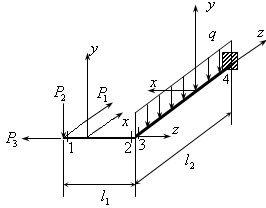
Рис.19.1

Вычислим силы и моменты в четырех сечениях (см. рис.19.1).

Рассмотрим сечение 1 (в левом конце стержня длины ): .

Найдем силы и моменты в сечении 2:

.

Рассмотрим сечение 3:

.

Находим силы и моменты в сечении 4:

.

Поскольку на втором участке сверху действует погонная сила q, то эпюра будет криволинейной и вогнутой.

Строим эпюры сил и моментов по следующим правилам.

1. Знаком снабжается только эпюра . Силу откладываем перпендикулярно оси стержня в произвольном направлении, снабжая знаком «-», если участок сжимается.

2. Крутящий момент откладываем также в произвольном направлении, но без знака.

3. Если рассматривается воздействие на сечение левой части бруса и если суммы внешних сил положительны, то тоже положительны и откладываются в направлении осей x,y (и наоборот, если рассматривается действие на сечение правой части бруса, то положительные внешние силы дают отрицательные вклады в ).

4. Моменты откладываются на растянутых волокнах и знаком тоже не снабжаются. Важное правило: откладываем в плоскости действия сил и моментов, которые их вызывают. Например, в нашем случае -по вертикали, - по горизонтали.

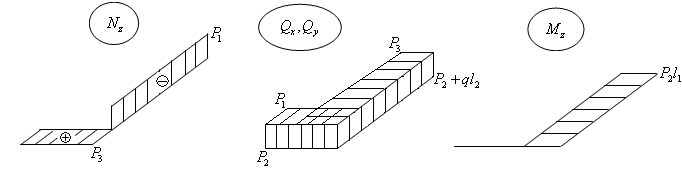
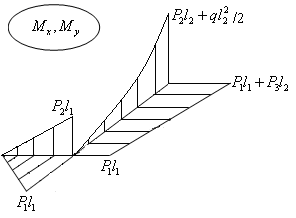
Рис.19.2

Опасным называется сечение, в котором или , или принимают экстремальные значения.

Из эпюры видно, что в нашем случае на первом участке опасным является сечение, которое находится на стыке двух участков, на втором участке опасным является сечение, расположенное в заделке.

По эпюрам определяют вид деформации: 1-ый стержень испытывает растяжение с изгибом, 2-ой испытывает сжатие и кручение с изгибом.