18. Кручение валов

18.1. Кручение круглых валов

Брусья круглого сечения, которые в конструкциях работают на кручение, часто называют валами. Примером закрученных брусьев являются, например, стойки рекламных щитов (рис.18.1).

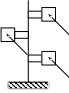
Рис.18.1.

Возникают 2 задачи:

1. Проверка прочности валов (т.е. не возникнет ли опасности разрушения вала при заданных нагрузках).

2. Проверка жесткости валов (т.е. не слишком ли он сильно деформируется при заданных нагрузках).

18.2. Напряжения в сечениях вала

Рассмотрим сечение I-I (см. рис.18.2). Считаем вал состоящим из двух частей - левой и правой. Левая часть действует на правую некоторым моментом (у нас это М_z = m₁ – m₂).

Определение. Суммарный момент, которым левая часть вала воздействует на првую (или наоборот), называется крутящим моментом (обозначается или ). Это определение дает правило вычисления : крутящий моментом равен сумме моментов, которые действует слева или справа от сечения.

Правило знаков для крутящих моментов. Хотя для прочностных расчетов знак крутящего момента не имеет значения, но для определенности его можно ввести таким же образом, как и в теоретической механике. А именно, вклад внешнего момента (например, т₃ на рис.18.2) в крутящий момент положителен, если он действует справа и переводит ось «х» в ось «у» против часовой стрелки при условии, что мы смотрим с положительного конца оси z. Например, на первое сечение действует .

Рассечем теперь вал плоскостью II-II (рис.18.2). Тогда

.

Можно подсчитать по другому. Например, для второго сечения:

Здесь принят знак – ввиду того, что на сечение мы смотрим не с конца стрелки z.

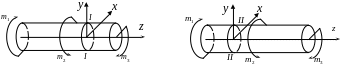
Рис.18.2

Это дает одно и то же, так как из условия равновесия вала следует, что:

.

Закон распределения касательного напряжения

Поскольку правая часть воздействует на сечение I-I не в одной точке, а по всему сечению, то картина воздействия будет такая, как это изображено на рис.18.3.

Рис.18.3

Распределенное воздействие правой частью бруса на плоскость сечения по определению будет касательным напряжением .

Выяснить закон распределения в сечении можно разными способами. Рассмотрим сначала первый (не традиционный) способ.

Из рассмотрения рис.18.3 можно заключить, что в силу симметричности сечения напряжение зависит только от расстояния до центра. Тогда можно записать:

.

Разложим функцию в ряд Маклорена:

Поскольку мы рассматриваем тела типа брусьев, у которых размеры поперечного сечения много меньше длины, то будет малой величиной по сравнению с длиной вала. Поэтому можно отбросить малые слагаемые в разложении и записать:

.

Теперь рассмотрим малый элемент около центра сечения:

Из рисунка видно, что при стремлении размера элемента к нулю напряжение τ в одной и той же точке должно быть направлено и вверх, и вниз, и влево, и вправо. Это возможно, если только оно равно там нулю:

.

Отсюда следует, что коэффициент k₀ = 0. Таким образом, закон распределения в сечении имеет вид

. (18.3)

Теперь приведем второй, традиционный способ. Для этого проводят следующие рассуждения. Вырежем диск толщины а (рис 18.3). Из этого диска радиуса R, вырежем малый диск радиуса .

Рис.18.4

Рассмотрим прямоугольник . При кручении точка перемещается в точку , точка перемещается в точку . Видим, что получит сдвиг.

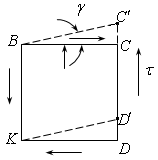
Рис.18.5

Из рисунка видно, что:

(18.2)

Здесь в силу малости .

Выразим теперь через радиус (см. рис.18.4).. Введем центральный угол . Тогда

. (18.3)

Приравнивая (18.2) и (18.3) находим:

.

По закону Гука: .

Обозначая снова получаем

.

Выводы:

1. Распределение по сечению не равномерное, а именно: в центре 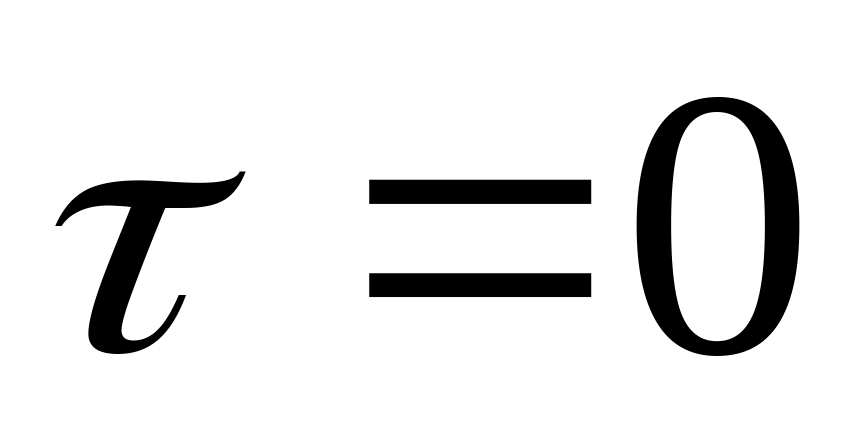, так как .

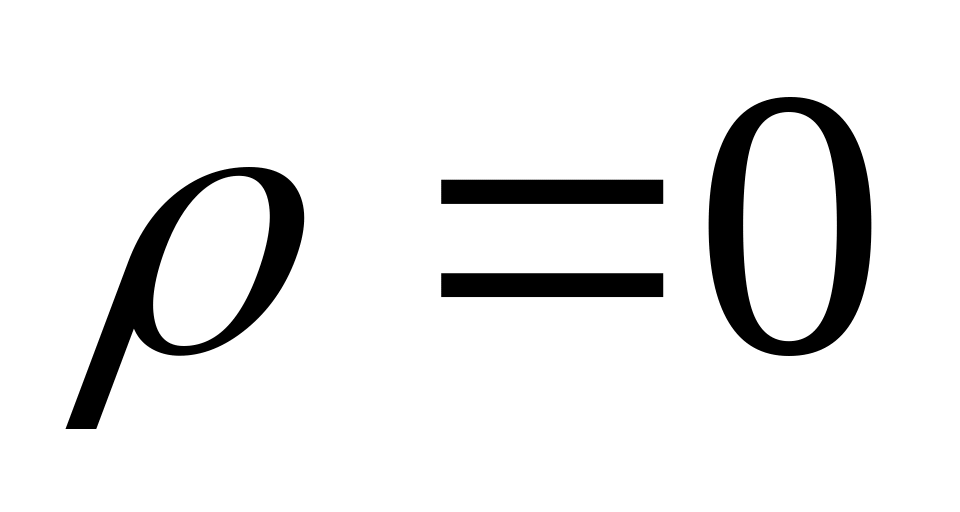2. Наибольшее напряжение возникает на малых площадках, примыкающих к поверхности (при ), т.е.

.