15. Изгиб балок

15.1. Нормальные напряжения. Формула Навье

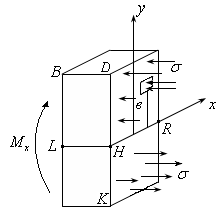
Рассмотрим элемент изогнутой балки (рис. 15.1-15.2)

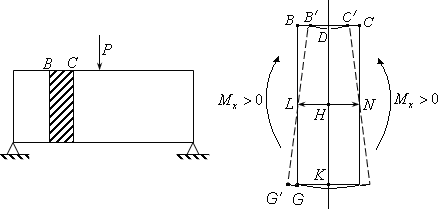
Рис.15.1 Рис. 15.2

Здесь - момент внешних сил, которые воздействуют на наше сечение слева или справа (по определению он называется изгибающим моментом).

Из рис. 15.2, что верхние волокна укорачиваются (например, ВС), а нижние - удлиняются. Между ними есть волокно LN, которое не деформируется (рис.15.2). Очевидно, что чем дальше волокна от LN, тем больше удлинение волокон, значит по закону Гука и сила их растяжения больше. Таким образом, максимальное напряжение будет там, где волокна наиболее удалены от .

Для вывода формулы вычисления напряжений используем метод сечений. Рассмотрим поперечное сечение DК (рис.15.2, 15.3)). Проведем ось х через точку Н (рис 15.3). На этой линии, напряжений не будет.

Определение: Линия HR, на которой нет напряжений, называется нейтральной.

Таким образом, ось будет лежать на нейтральной линии, так как на ней (для удобства записи индексы для напряжений σ_z , τ_zy в дальнейшем будем опускать).

На верхнюю часть нашего элемента правая часть балки действует сжимающим напряжением , а на нижнюю - растягивающим (см. рис.15.3).

Разобьем сечение на малые микроплощадки dA. Рассмотрим одну из них. На неё с правой стороны действует следующая сжимающая сила:

(15.1)

Рис. 15.3

Относительно оси сила имеет плечо , следовательно, создаёт момент: dM = в dN. (15.2) Из рисунка видно, что плечо в - это координата центра микроплощадки . Значит в = у. Тогда: . (15.3)

Суммируя, получаем результирующий момент , который создают напряжения :

(15.4)

Поскольку вся балка находится в покое, то и любой его элемент тоже статичен. Следовательно, можно записать уравнение статики и для элемента, изображенного на рис.15.3. Запишем его в виде:

.

Отсюда:

. (15.5)

Для отыскания из (15.5) учтем, что чем дальше микроплощадка от , тем больше . То есть, чем больше в, тем больше . Учитывая, что в = у, эту фразу можно записать в виде:

. (15.6)

Здесь - коэффициент пропорциональности, а знак «-» поставлен потому, что при (т.е. в верхней части) действуют сжимающие напряжения.

Примечание. Соотношение (15.6) можно считать первым членом разложения функции σ в ряд Маклорена по аргументу у.

Найдем (тогда мы будем знать формулу для ).

Подставим в (15.5), тогда:

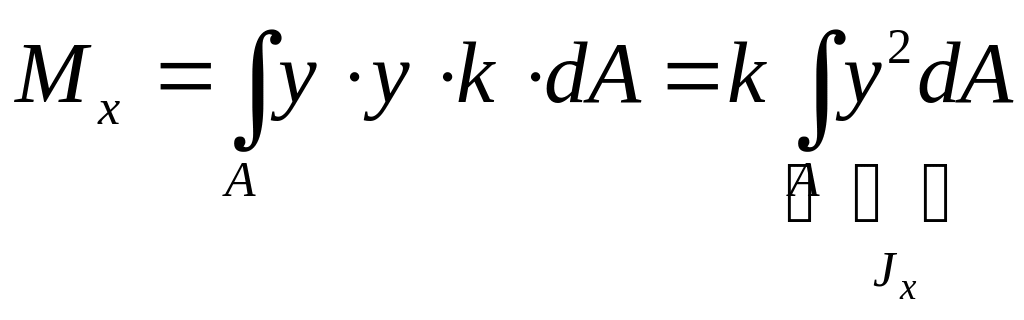. (15.7)

Согласно определению - это момент инерции сечения. Таким образом,

.

Окончательно формула для принимает вид:

. (15.8)

Здесь у - это координата точки (микроплощадки ), в которой вычисляется напряжение, -осевой момент инерции сечения. Формулу (15.8) нередко называют формулой Навье.

Примечание. Согласно закону Гука по формуле (15.6) получим, что . Это означает, что линия GG′ - прямая. Эксперимент подтверждает этот вывод для длинных балок. Тогда в рассуждениях можно пойти дальше и считать, что сечение со следом ВG остается плоским. Это предположение называют гипотезой Бернулли. Его обычно принимают за исходное положение. Тогда формула (15.6) будет следствием гипотезы Бернулли.