14. Усталостное разрушение (циклическая прочность)

Всем известно, что проволоку можно разрушить путем многократного изгиба. Это явление называется усталостным разрушением.

Изобразим действие нагрузки во времени графически (рис 14.5).

Рис 14.1.

Различают симметричный цикл (изгиб осей автомобиля, вагона и т. п.), изображенный на рис.14.1 слева, и несимметричный цикл, изображенный справа. Симметричный цикл наиболее опасный, поэтому несимметричный цикл иногда рассматривают как симметричный (такой подход называется расчетом в запас прочности).

14.1. Расчет сооружений при циклическом нагружении с помощью диграммы Вёлера

Рассмотрим традиционный способ расчета на усталость при симметричном цикле. Сначала из эксперимента определяют число циклов N, которое приводит к разрушению образцов из данного материала при ряде значений напряжений. После этого строят диаграмму Вёлера (рис 14.2).

Рис 14.2

При известной диаграмме Вёлера можно приступать к расчету сооружения или конструкции на усталость. Для этого находят напряжение в наиболее загруженной области конструкции, то есть находят . Затем по диаграмме Вёлера отыскивают предельный цикл N*. Уменьшая его на коэффициент запаса k , получаем допустимое значение циклов , которое называют также ресурсом изделия.

Поскольку время одного цикла (т.е., период) обычно известно, то время, которое обеспечивает прочность конструкции, находится по формуле:

. (14.1)

Примечание. Для некоторых материалов (например, для стали) на диаграмме существует механическая характеристика , которая называется пределом выносливости. Если рабочее напряжение σ не превышает значения , то разрушения не происходит ни при каких N. Поэтому, если нет требований экономичности изделии, то условие прочности при циклической нагрузке записывают просто в виде (k – коэффициент запаса):

.

14.2. Расчет сооружений при циклическом нагружении по теории развивающихся трещин

Ц иклическая нагрузка приводит к развитию трещин во времени. Из экспериментов выявлено, что скорость подрастания трещины тем больше, чем больше размах напряжения растяжения и чем больше длина трещины.

Обозначим через - скорость подрастания трещины, то есть:

. (14.2)

Итак, тем больше, чем больше размах напряжения растяжения и чем больше длина трещины b. Это утверждение можно записать в виде:

. (14.3)

Здесь В, m, n – механические характеристики материала.

Эксперименты показывают, что для всех материалов степень n в два раза меньше чем m, т.е. . Тогда:

(14.4)

Это соотношение называется законом роста трещины.

Если напряжение изменяется во времени, т.е. , то закон запишется в виде:

(14.5)

Это дифференциальное уравнение относительно длины трещины b. Оно решается методом разделения переменных:

. (14.6)

Отсюда получим:

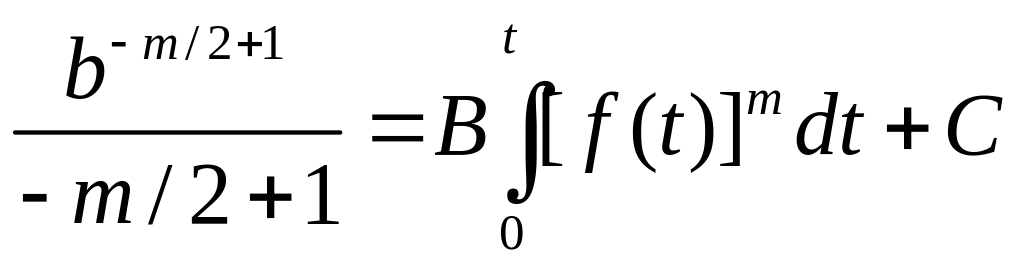. (14.7)

Константу С определяют из начальных условий, т.е. из условия, что в начальный момент времени длина трещины известна. Пусть при t = 0 начальная длина трещины равна b₀. Тогда

. (14.8)

Рассмотрим случай, когда можно считать, что размах напряжения постоянен, то есть

f(t) = const=Δσ_o.

Из (14.7) вытекает выражение

. (14.9)

Таким образом, в любой момент времени можно вычислить длину трещины.

Согласно формуле Гриффитса, зная длину трещины можно найти предел прочности , при котором произойдет разрушение:

.

Здесь Е модуль Юнга, а - механическая характеристика материала.

Подставляя найденную длину трещины b в условие разрушения , получаем уравнение для отыскания времени разрушения t^*:

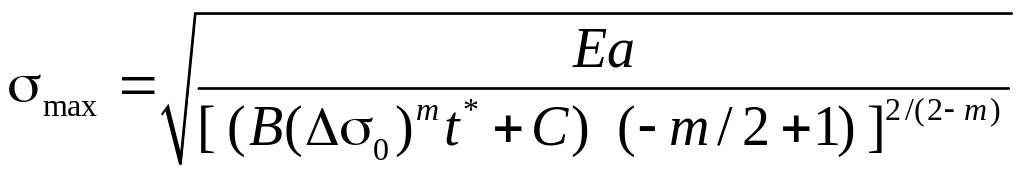. (14.10)

Отсюда находим t^*:

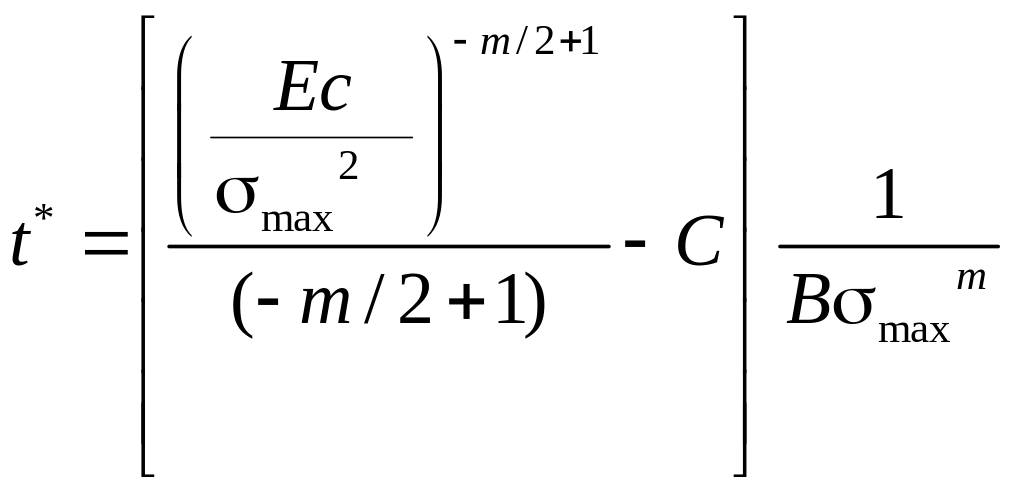
Перечислим использованные обозначения: константы Е, m, а, В являются механическими характеристиками материала, - размах напряжения растяжения элемента, константа С определяется по формуле (14.8), в которой - первоначальная длина трещины.

Уменьшая t* на коэффициент запаса k , получаем [t] - допустимое значение времени эксплуатации сооружения.