11.5.4.Четвертая теория (энергетическая)

Она наилучшим образом согласуется с экспериментальными данными для пластичных материалов типа сталь. Утверждается, что элемент тела единичного объема разрушится тогда, когда работа максимальных касательных напряжений достигнет предельного значения.

Для трехосного напряженного состояния, как было отмечено в ранее в разделе 11.5.3, в разных плоскостях имеем 3 разных :

Рассмотрим работу касательного напряжения на перемещении ВВ′.

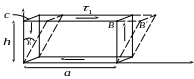
Рис.11.16

Имеем:

Работа силы на перемещении ВВ′ будет (здесь и в дальнейшем учтено, что напряжения не сразу достигают своих окончательных значений, а возрастают, начиная с нуля, вследствие чего появляется множитель 0.5):

.

В виду малости угла сдвига имеем:

.

Примем, что объем элемента равен единице :

Таким образом, получаем:

.

По закону Гука ( - модуль сдвига):

.

Окончательно получим:

.

Аналогично, максимальные касательные напряжения в других плоскостях дают работы:

, .

Суммируя их, получим:

.

Обозначим работу внутренних сил, приводящих к разрушению элемента тела, через .

Тогда критерий разрушения можно записать в виде:

.

Выразим правую часть через . Рассмотрим частный случай - одноосное растяжение. Тогда в момент разрушения:

.

Подставляя в критерий разрушения, получим:

Эта теория также справедлива только для материалов, у которых пределы прочности на растяжение и сжатие одинаковы. Для них обозначение для предела прочности, как и в III теории, применяют без индексов «^раст», «^сж»:

Окончательно четвертая теория теперь примет вид:

. (11.13)

Рассмотрим теперь частный случай, когда = 0, который имеет место в балках и плитах строительных сооружений. Тогда получим критерий в виде:

.

или

(11.14)

Предельная кривая в системе координат примет вид эллипса, приведенного на рис.11.15.

Четвертая теория хорошо подтверждается для материалов типа сталь, алюминий и т.п. Недостатком ее является то, что она справедлива только при предположении, что пределы прочности материала на растяжение и сжатие одинаковы. Ее называют иногда критерием Мизеса.

11.5.5. Пятая теория – критерий Мора

Ф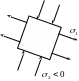 ормулируется для элемента тела, который растягивается в продольном направлении и сжимается в поперечном направлении (см. рис.11.17).

Рис.11.17 Рис.11.18

Для большинства материалов (в том числе, для бетона) было обнаружено, что образцы, предварительно сжатые в поперечном направлении напряжением σ₂ (см. рис.11.18), разрушаются при напряжении σ₁, которое меньше (предела прочности при простом растяжении в продольном направлении).

Запишем это утверждение аналитически. Учтем, что при растяжении , при поперечном сжатии . Тогда разрушение произойдет, если

,

где n > 0 – некоторый коэффициент. Выразим n через пределы прочности материала. Для этого сначала рассмотрим разрушение при простом сжатии, полагая, что образец доведен до разрушения. Тогда:

Подставляя в условие разрушения, получим

Отсюда: .

Таким образом, для элемента тела, который растягивается в продольном направлении и сжимается в поперечном направлении, получим критерий Мора в виде:

.

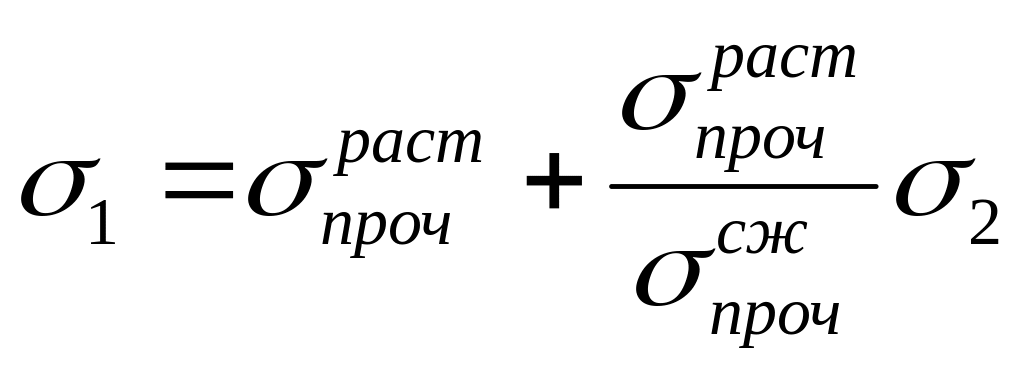В 1-ой и 3-ей четвертях (т.е. при растяжении или сжатии в обоих направлениях) применяют первую теорию. Предельная кривая примет вид многоугольника, приведенный на рис.11.19.

Рис.11.20

Примечание1.

Если на элемент тела кроме действует еще и , при этом , а также , , то критерий Мора записывают том же виде

.

Это означает, что влиянием на прочность элемента пренебрегают.

Примечание2.

Из сравнительного анализа третьей теории прочности и критерия Мора видно, что третья теория является его частным случаем, когда пределы прочности на растяжение и сжатие одинаковы, т.е. при .