11.5.1.Первая теория прочности

Рассмотрим малый элемент тела с гранями, совпадающими с главными площадками (см.рис.11.11). Пусть . Тогда утверждается: какими бы не были , элемент разрушается тогда, когда достигает предела прочности на растяжение .

(11.9)

Если же , то разрушение происходит при .

Если имеет место сжатие (то есть ), то условия разрушения принимается в виде: .

Предельная кривая для первой теории имеет вид, изображенный на рис.11.13.

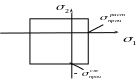
Рис.11.13

Недостатки теории:

1. Теория утверждает, что якобы наличие поперечного напряжения 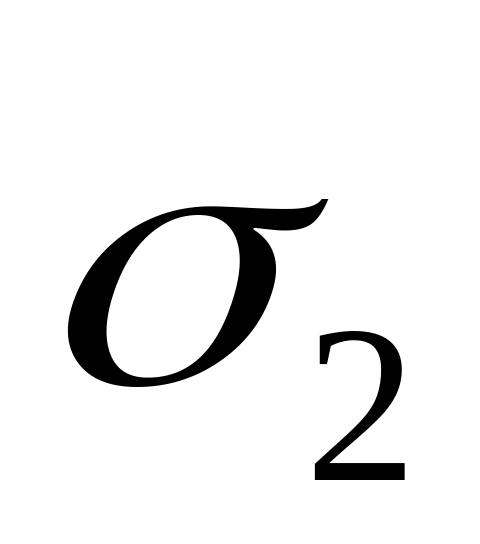совсем не влияет на прочность материала в продольном направлении, что не подтверждается экспериментами для большинства материалов.

2. Она удовлетворительно подтверждается только для некоторых

хрупких материалов, причем, для растягивающих напряжений. Например, экспериментальные данные хорошо подтверждают эту теорию в первом квадранте для чугуна.

11.5.2.Вторая теория прочности

Утверждается, что разрушение элемента наступает тогда, когда максимальная деформация удлинения достигает предельного значения , то есть или тогда, когда

или же когда

.

В компонентах это условие записывается с помощью закона Гука:

, (11.10)

Тогда получим: .

Выразим С через . Для этого учтем, что это условие должно быть справедливо и при разрушении простым растяжением. Тогда:

Таким образом, вторая теория примет вид:

или (11.11)

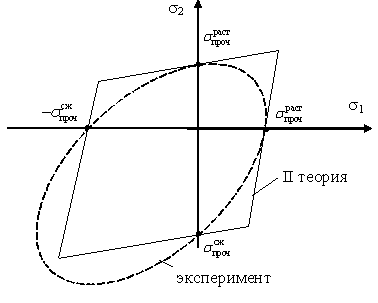
Рис.11.14

А налогичные соотношения получим при деформации укорочения:

или

Предельная поверхность примет вид, изображенный на рисунке 11.14 в виде многоугольника. Вторая теория плохо коррелирует с экспериментом.

11.5.3.Третья теория прочности (теория максимальных касательных напряжений)

Эта теория удовлетворительно согласуется с экспериментами над материалами, у которых пределы прочности на растяжение и сжатие одинаковы (например, для стали). Поэтому в дальнейшем будем считать, что = . Для таких материалов обозначение для предела прочности применяют без индексов «^раст», «^сж»:

Кроме того, будем считать, что напряженное состояние – трехосное.

Согласно III теории, утверждается, что разрушение наступит тогда, когда в каком-то элементе достигнет предельного значения, то есть когда:

.

Как было получено ранее, максимальные касательные напряжения возникают на площадках, наклоненных под углом 45^о к направлению действия , и определяются по формуле:

.

Выразим через . Условие прочности должно быть справедливо и при разрушении простым растяжением, т.е. тогда, когда:

Тогда . Из условия прочности вытекает, что:

(11.12)

Аналогичные максимальные касательные напряжения возникают на площадках, наклоненных под углом 45^о к направлению действия , и . Они определяются по формулам

, .

Таким образом, окончательно условие потери прочности примет вид:

или

или

или

В строительстве при расчете балок, плит перекрытия, балок стенок считается, что , т.е. напряжения возникают только в плоскости , Тогда из напряжение будет наибольшим только тогда, когда имеют различные знаки, т.е. во 2-ой и 4-ой квадрантах. Если же имеют одинаковые знаки (в первой и третьей квадрантах), то получим, что или . Подставляя в условие прочности , получим

или Таким образом, в первой и третьей квадрантах третья теория прочности совпадает с первой. Предельная кривая в частном случае, когда =0, примет вид шестиугольника, приведенного на рис.11.15.

Рис.11.15