11.3. Главные напряжения

Рассмотрим общий случай воздействия на элемент тела напряжений . Для этого сложим правые части формул для и получим :

(11.7)

Аналогично найдем

(11.8)

Эти формулы подобны формулам для осевых и центробежных моментов инерции для повернутых осей. Поэтому точно так же вводятся и понятия главных напряжений и главных площадок, т.е. следующим образом. Вычислив для разных углов, можно найти максимальное и минимальное их значения. Эти напряжения называются главными. Обычно обозначают:

Главные площадки – это сечения, на которых экстремальны.

Угол , который определяет положение главных площадок, получаем по теореме Ферма: при должно быть

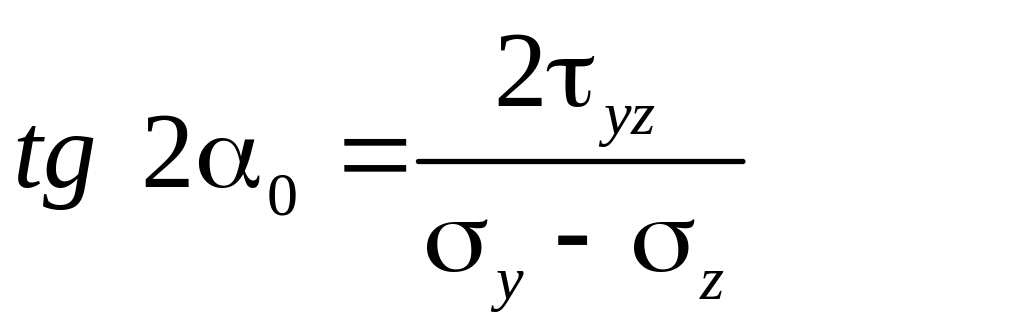
Отсюда находим .

Аналогично теории геометрических характеристик можно видеть, что на этих главных площадках касательных напряжений не будет, т.е.

.

Следствие:

Всегда можно найти в теле такое положение малого элемента, в котором он только растягивается или сжимается в двух перпендикулярных направлениях, причем эти напряжения будут экстремальными.

Примечание: согласно свойствам , если взять угол , то условие снова удовлетворится. Таким образом, существуют 2 главные площадки под углами и .

Вычисление

В некотором теле найдем главные площадки для малого элемента.

Рис.11.7 Рис.11.8

Оси, ортогональные главным площадкам, обозначим . На главных площадках , как было сказано выше.

Рассмотрим площадку под углом . Используя формулу (11.8) для при получим:

Поскольку , то

Таким образом, возникает на площадках, расположенных под углом к главной площадке

Можно показать, что в случае, когда действуют лишь напряжения значения главных напряжений можно вычислять даже не зная положения главных площадок по формулам:

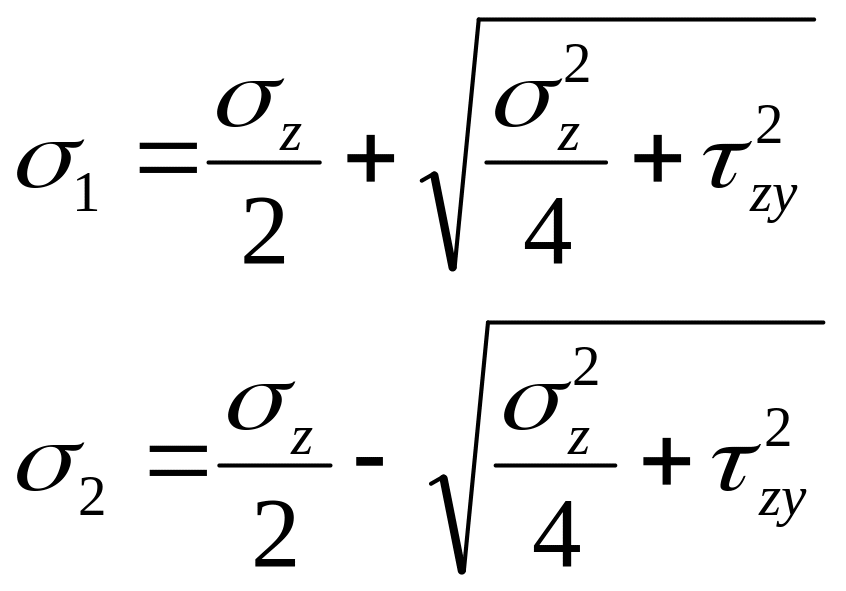
Тогда: .

11.4. Виды разрушений материалов

Разрушение подразделяют на хрупкое и вязкое.

Хрупкое разрушение – это разрушение, при котором материал разрушается (делится на части) от развития трещин (см. рис.11.9).

.

Рис.11.9

Вязкое разрушение – это разрушение путем сдвига частиц друг относительно друга (например, одна часть бруса скользит относительно другой, как это показано на рис.11.10).

Рис.11.10

11.5.Теории кратковременной прочности

Исторически наиболее популярными были пять теорий прочности. Однако некоторые из них плохо подтверждаются экспериментом, поэтому на сегодня не применяются или применяются лишь в частных случаях.

Если в теле ненулевыми являются, например, только , а остальные напряжения равны нулю, то говорят, что тело находится в плоском напряженном состоянии. В общем случае напряженное состояние называют трехосным. Поскольку в строительных сооружениях плоское напряженное состояние имеет место в подавляющем большинстве случаев, то ниже для простоты будем рассматривать лишь это состояние (там, где это возможно). Кроме того, при изложении IV и V теорий ниже приводятся более простые способы вывода критериев разрушения по сравнению с традиционными.

Вырежем из тела малый элемент с гранями, параллельными главным площадкам. Так как - главные, то касательных напряжений нет.

Рис.11.11

Основная проблема, которая обсуждается в теориях прочности, заключается в следующем.

Пусть известен предел прочности при одноосном нагружении элемента только напряжением (см. рис.11.11). Вопрос – увеличится, уменьшится или не изменится прочность элемента, если предварительно нагрузить его в поперечном направлении напряжением ? Другими словами, какое значение напряжения потребуется для того, чтобы разрушить образец - меньшее, чем , большее, чем , или же равное ? Оказалось, что однозначного ответа на этот вопрос нет, так как для различных классов материалов степень влияния разная, причем может как повышать прочность, так и понижать ее, а иногда на прочность в направлении действия оно никак не влияет.

Введем понятие предельной кривой, с помощью которой ответ на этот вопрос можно получить графически.

Проведем ряд экспериментов при разных комбинациях и доведем образец до разрушения. Сведем результаты в таблицу, например, в виде:

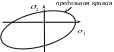
Рис.11.12

Отложим эти значения в системе координат (рис.11.12). Получим ряд точек. Соединяя их, получим некоторую кривую замкнутой формы, которая называется предельной кривой.

МПа	400	300	-210	…
МПа	150	250	-170	…

Если имеется напряжение и в третьем направлении, то получим уже предельную поверхность.

Смысл предельной кривой в том, что если комбинация образует точку внутри кривой, то разрушения не происходит, а если проектные окажутся на кривой или вне нее, то материал не выдержит эту комбинацию напряжений. Ниже рассмотрим различные случаи предельных кривых.

Примечание. Так как осуществить многоосное нагружение достаточно трудно, то для построения предельной поверхности часто применяли различные обобщения условий прочности для плоского напряженного состояния.