9.6.1. Долговечность железобетонной колонны при наличии ползучести бетона
Как и ранее метод определения ее ресурса рассмотрим на примере железобетонной колонны (см. рис.9.6.1.).
Пусть как и ранее: . Примем, что арматура чисто упругий элемент, а бетон является вязким, то есть ползет (см. раздел 8.1) по закону:
|
Рис. 9.7 |
(9.9)
Упругая часть деформации определяется по закону Гука:
Найдем
сначала
напряжения
в бетоне
и в арматуре
,
а затем из условия прочности определим
время, до которого оно будет выполняться.
Поскольку ползучесть происходит во времени, то напряжения и деформации тоже являются функциями времени t:
.
Часть силы F распределяется на бетон, часть на арматуру:
(9.12)
Решений бесконечное множество, для выбора из них соответствующего задаче нужно привлекать дополнительное условие. Как и ранее имеем:
(9.13)
В (9.13) подставим нижеследующие соотношения:
.
Продифференцируем условие совместности (9.13) по времени:
.
Подставим
сюда
в
соответствии с законом ползучести
(9.9):
(9.14)
Исключим
отсюда
.
Для этого используем связь усилий и
напряжений:
Тогда из (9.14) вытекает, что:
.
Деля на площадь арматуры, получим:
. (9.15)
Продифференцируем это соотношение по t:
Теперь
подставим
это
в (9.14):
.
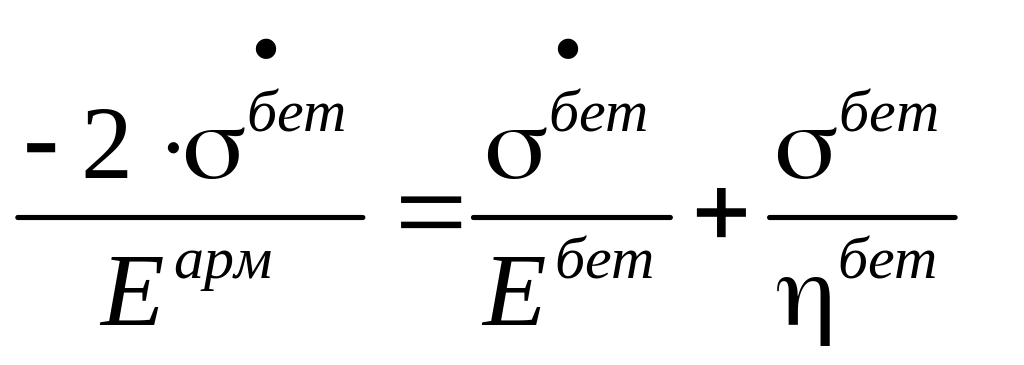Получили
дифференциальное уравнение относительно
неизвестной
.
Умножая его на
и деля на 7 получим:
.
Решение его известно и имеет вид:
(9.16)
Константу С
находят из каких-либо известных условий,
а именно нам известны
в начальный момент времени (см. задачу
9.1), т.е. при
можно записать:
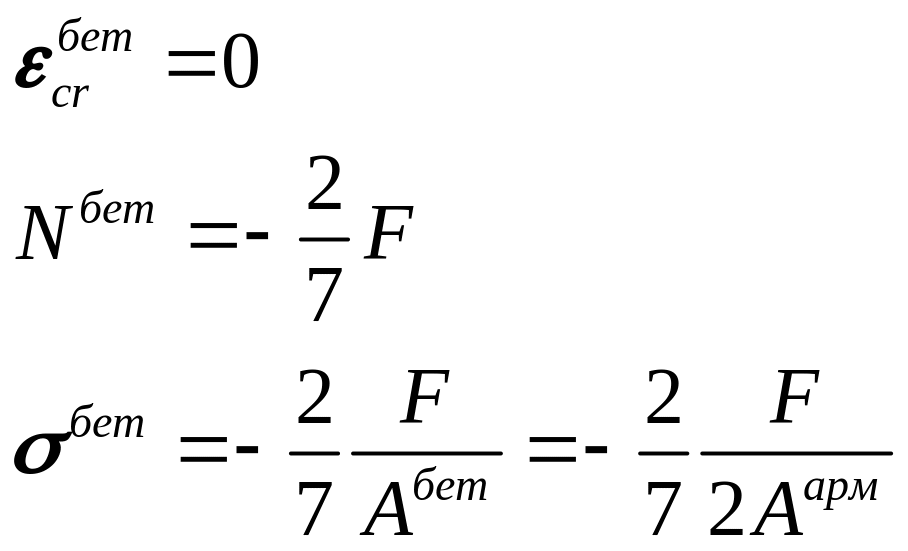
Подставим в (9.16):
.
Полученное С
подставляем в (9.15). Учитывая, что
находим:
.
Анализ решения:
Из последнего
выражения видно, что при больших
напряжение
становится
все меньше и меньше, т.е. стремится к
нулю.
Таким образом, с течением времени бетон разгружается.
Определение: такое явление называется релаксацией или отдыхом материала.
Арматура, напротив,
в это время догружается, значит при
больших
получим, что
,
т.е. вся нагрузка будет приходиться на
арматуру.
Проведем теперь расчет на долговечность. Под термином долговечность будем понимать время t*, в течение которого удовлетворяются условия прочности. Имеем:
Поделим на
,
тогда получим:
Пусть в момент
в арматуре напряжение
достигает предела прочности σ*
(ниже учтено, что при сжатии напряжения
отрицательны):
.
Перенося первое слагаемое вправо и логарифмируя это уравнение, получим:
.
Отсюда:
.
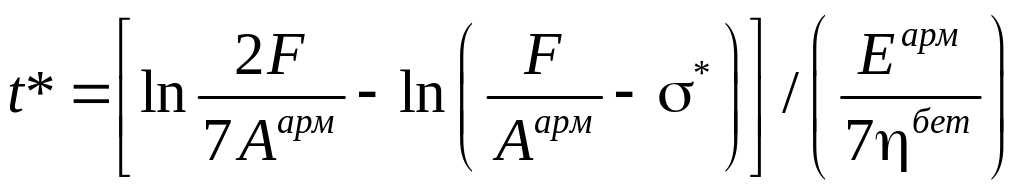Это
и есть время, по достижении которого
произойдет разрушение арматуры. Из
решения видно, что это произойдет только
в том случае, если сила F
достаточно велика, а именно, если
выражение под логарифмом будет
положительно, т.е. при
.
Очевидно также, что сила F
не должна
быть и слишком большой, при которой
произойдет мгновенное разрушение. Это
будет тогда, когда t*=0,
т.е., когда квадратная скобка равна
нулю.