9. Примеры использования законов механики для расчета строительных сооружений

9.1. Расчет статически неопределимых систем

9.1.1. Статически неопределимая железобетонная колонна

Рассмотрим бетонную колонну с металлической арматурой, нагруженную через жесткую плиту силой F (рис.9.1). Примем следующие исходные данные (они приняты таковыми только для демонстрации метода отыскания продольных сил сжатия).

Рис.9.1

Д ано:

Найти: Силу сжатия бетона и силу сжатия арматуры .

Решение: Возьмем сечение:

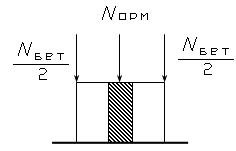
Рис.9.2

На это сечение сила давления F распределяется не одинаково, хотя суммарно имеет место равенство:

- (9.1)

Здесь знак «-» поставлен потому , что имеет место сжатие сечения. Уравнение (9.1) имеет бесконечное множество решений. Уравнений равновесия для однозначного определения сил сжатия бетона и арматуры записать не удается. Поэтому задача называется статически неопределимой. Поскольку методами теоретической механики выбрать решение, отвечающее реальности, невозможно, то для этого используем свойство тел деформироваться по закону Гука, т.е. кинематические соображения. Из рисунка рис.9.1 видно, что и бетон, и арматура укорачиваются одинаково, т.е.

Это соотношение называется уравнением совместности деформации.

Подставим сюда закон Гука.

.

Найдем соотношение знаменателей:

.

Тогда получим:

.

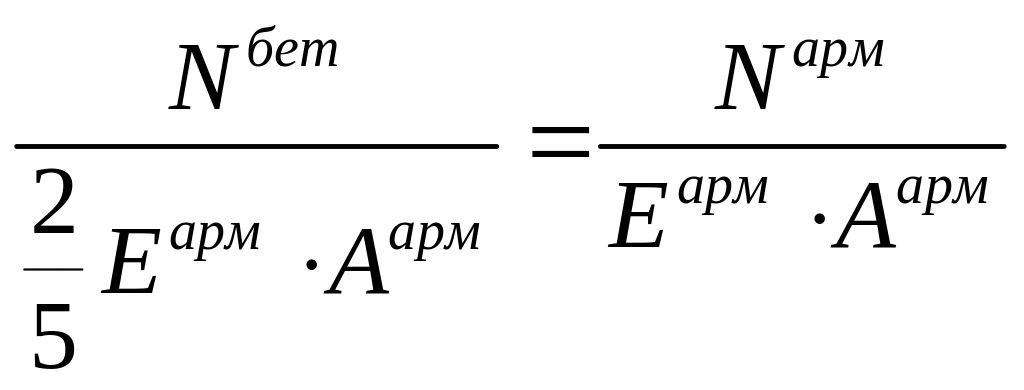Отсюда

.

Подставляя в (9.1) найдем:

.

Отсюда:

Вывод: хотя арматуры в колонне в два раза меньше чем бетона, но она воспринимает основную часть нагрузки (а именно - 71% нагрузки).

9.1.2 Температурные напряжения

Рассмотрим ту же колонну, но не нагруженную. Пусть в ней произошел перепад температуры на 100. Примем следующие исходные данные (они снова приняты таковыми только для демонстрации метода отыскания температурных напряжений).

Дано:

Найти:

Решение:

От перепада температур в несвязанных арматуре и бетоне деформации были бы разные. Но в колонне они воздействуют друг на друга, следовательно:

.

С другой стороны, колонна не нагружена, следовательно, нет суммарных сил сжатия на любые сечение, поэтому:

(9.2)

Поскольку неизвестных два, а уравнение одно, то снова привлечем геометрические соображения. Из рисунка видно, что и бетон, и арматура могут укорачиваться только одинаково. Тогда:

(9.3)

Запишем выражения для удлинений с учетом закона Гука и Дюгамеля-Неймана:

Подставим в условие совместности деформации (9.3). С учетом исходных данных получим:

.

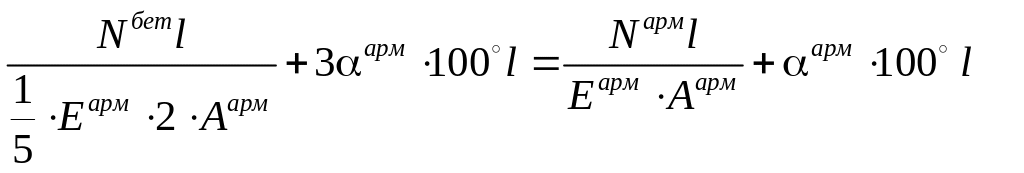Умножая на и учитывая исходные данные, получим:

(9.4)

Таким образом, имеем систему уравнений (9.2), (9.4):

Решая, получим:

.

Знак «+» говорит о том, что арматура растянута. Из (9.2) вытекает, что , следовательно, бетон сжат.

Отметим следующий интересный факт. Хотя бетон сжат, но ввиду нагрева вся колонна, а значит и бетонная ее часть, удлинились.

Действительно, подсчитаем:

Знак «+» говорит о том, что колонна удлинилась.

Можно подсчитать напряжения:

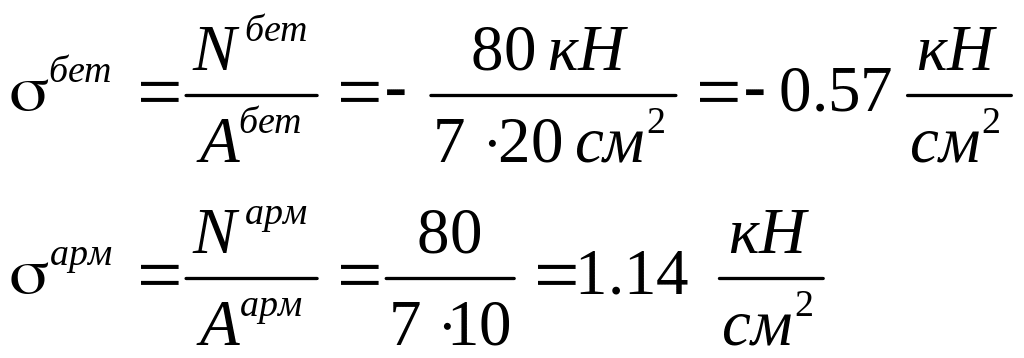
Видно, что арматура является в два раза более нагруженной, чем бетон.