5. Закон сохранения энергии.

Рассмотрим нагруженный брус

Рис.8.4

Введем понятие перемещения точки, например,

- вертикальное перемещение точки В;

- горизонтальное смещение точки С.

Силы при этом совершают некоторую работу U. Учитывая, что силы начинают возрастать постепенно и предполагая, что возрастают они пропорционально перемещениям, получим:

.

Согласно закону сохранения: никакая работа не исчезает, она тратится на совершение другой работы или переходит в другую энергию (энергия – это работа, которую может совершить тело.).

Работа сил , тратится на преодоление сопротивления упругих сил, возникающих в нашем теле. Чтобы подсчитать эту работу учтем, что тело можно считать состоящим из малых упругих частиц. Рассмотрим одну из них:

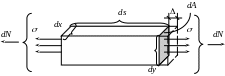
Рис.8.5

Со стороны соседних частиц на него действует напряжение . Равнодействующая напряжений будет

.

Под действием частица удлинится. Согласно определению относительное удлинение это удлинение на единицу длины. Тогда:

.

Вычислим работу dW, которую совершает сила dN (здесь также учитывается, что силы dN начинают возрастать постепенно и возрастают они пропорциональны перемещениям):

Для всего тела получим:

.

Работа W, которую совершило , называют энергией упругой деформации.

Согласно закону сохранения энергии:

6) Принцип возможных перемещений.

Это один из вариантов записи закона сохранения энергии.

Пусть на брус действуют силы F₁, F₂,…. Они вызывают в теле перемещения точки и напряжения . Дадим телу дополнительные малые возможные перемещения . В механике запись вида означает фразу «возможное значение величины а». Эти возможные перемещения вызовут в теле дополнительные возможные деформации . Они приведут к появлению дополнительных внешних сил и напряжений , δ.

Вычислим работу внешних сил на дополнительных возможных малых перемещениях:

Рис.8.6

Здесь - дополнительные перемещения тех точек, в которых приложены силы F₁, F₂, …

Рассмотрим снова малый элемент с поперечным сечением dA и длиной dz (см. рис.8.5. и 8.6.). Согласно определению дополнительное удлинение dz этого элемента вычисляется по формуле:

dz =  dz.

Сила растяжения элемента будет:

dN = (+δ) dA ≈  dA.

Работа внутренних сил на дополнительных перемещениях вычисляется для малого элемента следующим образом:

dW = dN dz =  dA  dz =   dV.

С уммируя энергию деформации всех малых элементов получим полную энергию деформации:

Закон сохранения энергии W = U дает:

.

Это соотношение и называется принципом возможных перемещений (его называют также принципом виртуальных перемещений). Аналогично можно рассмотреть случай, когда действуют еще и касательные напряжения. Тогда можно получить, что к энергии деформации W добавится следующее слагаемое:

.

Здесь  - касательное напряжение,  - сдвиг малого элемента. Тогда принцип возможных перемещений примет вид:

В отличие от предыдущей формы записи закона сохранения энергии здесь нет предположения о том, что силы начинают возрастать постепенно и возрастают они пропорционально перемещениям.

7) Эффект Пуассона.

Рассмотрим картину удлинения образца:

Рис.8.7

Явление укорочения элемента тела поперек направления удлинения называется эффектом Пуассона.

Найдем продольную относительную деформацию.

.

Поперечная относительная деформация будет:

.

Коэффициентом Пуассона называется величина:

.

Для изотропных материалов (сталь, чугун, бетон) коэффициент Пуассона

.

Это означает, что в поперечном направлении деформация меньше продольной.

Примечание. Современные технологии могут создать композиционные материалы, у которых коэффициент Пуассона >1, то есть поперечная деформация будет больше, чем продольная. Например, это имеет место для материала, армированного жесткими волокнами под малым углом <<1 (см. рис.8.8.). Оказывается, что коэффициент Пуассона при этом почти пропорционален величине , т.е. чем меньше , тем больше коэффициент Пуассона.

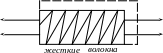
Рис.8.8 Рис.8.9

Еще более удивительным является материал, приведенный на (рис.8.9.), причем для такого армирования имеет место парадоксальный результат – продольное удлинение ведет к увеличению размеров тела и в поперечном направлении.

8) Обобщенный закон Гука.

Р ассмотрим элемент, который растягивается в продольном и поперечном направлениях. Найдем деформацию, возникающую в этих направлениях.

Вычислим деформацию , возникающую от действия :

.

От действия в результате эффекта Пуассона возникает дополнительная деформация:

.

Общая деформация будет:

.

Если действует и , то добавиться еще одно укорочение в направлении оси x .

Следовательно: .

Аналогично: .

.

Эти соотношения называются обобщенным законом Гука.

Интересно, что при записи закона Гука делается предположение о независимости деформаций удлинения от деформаций сдвига (о независимости от касательных напряжений, что одно и то же) и наоборот. Эксперименты хорошо подтверждают эти предположения. Забегая вперед, отметим, что прочность напротив сильно зависит от сочетания касательных и нормальных напряжений.

Примечание: Приведенные выше законы и предположения подтверждаются многочисленными прямыми и косвенными экспериментами, но, как и все другие законы, имеют ограниченную область применимости.