8.2. Основные законы, используемые в сопротивлении материалов

1. Соотношения статики. Их записывают в виде следующих уравнений равновесия.

2. Закон Гука (1678 год): чем больше сила, тем больше деформация, причем, прямо пропорционально силе. Физически это означает, что все тела это пружины, но с большой жесткостью. При простом растяжении бруса продольной силой N=F этот закон можно записать в виде:

.

Здесь продольная сила, l - длина бруса, А - площадь его поперечного сечения, Е - коэффициент упругости первого рода (модуль Юнга).

С учетом формул для напряжений и деформаций, закон Гука записывают следующим образом:

.

Аналогичная связь наблюдается в экспериментах и между касательными напряжениями и углом сдвига:

.

G называют модулем сдвига, реже – модулем упругости второго рода. Как и любой закон, имеет предел применимости и закон Гука. Напряжение , до которого справедлив закон Гука, называется пределом пропорциональности (это важнейшая характеристика в сопромате).

Изобразим зависимость  от  графически для стали Ст.3 (рис.8.1). Эта картина называется диаграммой растяжения. После точки В (т.е. при ) эта зависимость перестает быть прямолинейной.

При после разгрузки в теле появляются остаточные деформации, поэтому называется пределом упругости.

При достижении напряжением величины σ = σ_т многие металлы начинают проявлять свойство, которое называется текучестью. Это означает, что даже при постоянной нагрузке материал продолжает деформироваться (то есть ведет себя как жидкость). Графически это означает, что диаграмма параллельна абсциссе (участок DL). Напряжение σ_т, при котором материал течет, называется пределом текучести.

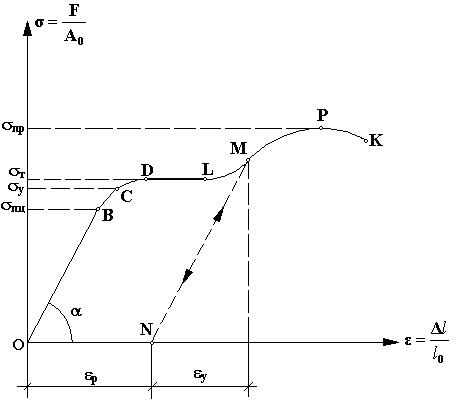
Рис.8.1

Некоторые материалы (Ст.3 - строительная сталь) после непродолжительного течения снова начинают сопротивляться. Сопротивление материала продолжается до некоторого максимального значения σ_пр, в дальнейшем начинается постепенное разрушение. Величина σ_пр - называется пределом прочности (синоним для стали: временное сопротивление, для бетона – кубиковая или призменная прочность). Применяют также и следующие обозначения:

σ_в , σ^*, R_b , R_bt.

Аналогичная зависимость наблюдается в экспериментах между касательными напряжениями и сдвигами.

3) Закон Дюгамеля – Неймана (линейного температурного расширения):

При наличии перепада температур тела изменяют свои размеры, причем прямо пропорционально этому перепаду температур.

Пусть имеется перепад температур . Тогда этот закон имеет вид:

.

Здесь α - коэффициент линейного температурного расширения, l - длина стержня, Δ l-его удлинение.

4) Закон ползучести.

Исследования показали, что все материалы сильно неоднородны в малом. Схематическое строение стали изображено на рис.8.2.

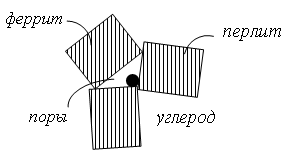
Рис.8.2

Некоторые компоненты материалов обладают свойствами жидкости, поэтому с течением времени образцы из таких материалов под нагрузкой получают дополнительное удлинение (рис.8.3.) (металлы при высоких температурах, бетон, дерево, пластики – при обычных температурах). Это явление называется ползучестью материала.

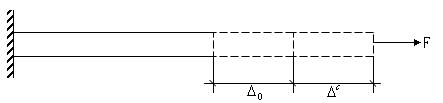
Рис.8.3

Для жидкости справедлив закон: чем больше сила, тем больше скорость движения тела в жидкости. Если это соотношение линейно (т.е. сила пропорциональна скорости), то можно записать его в виде:

.

Е сли перейти к относительным силам и относительным удлинениям, то получим

Здесь индекс «cr» означает, что рассматривается та часть удлинения, которая вызвана ползучестью материала. Механическая характеристика называется коэффициентом вязкости.